题目
例2 解不等式 |3x-1|leqslant 2.
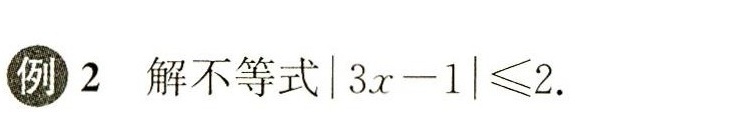
题目解答
答案

解析
考查要点:本题主要考查绝对值不等式的解法,需要将绝对值不等式转化为双重不等式进行求解。
解题核心思路:利用绝对值不等式的基本性质,将$|3x-1|\leqslant 2$转化为$-2 \leqslant 3x-1 \leqslant 2$,再通过逐步变形解出$x$的范围。
破题关键点:
- 正确转化绝对值不等式为双重不等式;
- 分步解双重不等式,注意运算过程中保持不等号方向不变。
步骤1:转化绝对值不等式
根据绝对值不等式性质,$|A| \leqslant a$($a > 0$)等价于$-a \leqslant A \leqslant a$。
因此,原式$|3x-1|\leqslant 2$可转化为:
$-2 \leqslant 3x-1 \leqslant 2.$
步骤2:解双重不等式
-
解左半部分:$-2 \leqslant 3x-1$
两边加1:
$-2 + 1 \leqslant 3x \implies -1 \leqslant 3x.$
两边除以3:
$-\dfrac{1}{3} \leqslant x.$ -
解右半部分:$3x-1 \leqslant 2$
两边加1:
$3x \leqslant 3.$
两边除以3:
$x \leqslant 1.$
步骤3:综合结果
将两部分结果合并,得到解集:
$-\dfrac{1}{3} \leqslant x \leqslant 1.$