题目
lim _(xarrow 1)(dfrac (2)({x)^2-1}-dfrac (1)(x-1)) ;
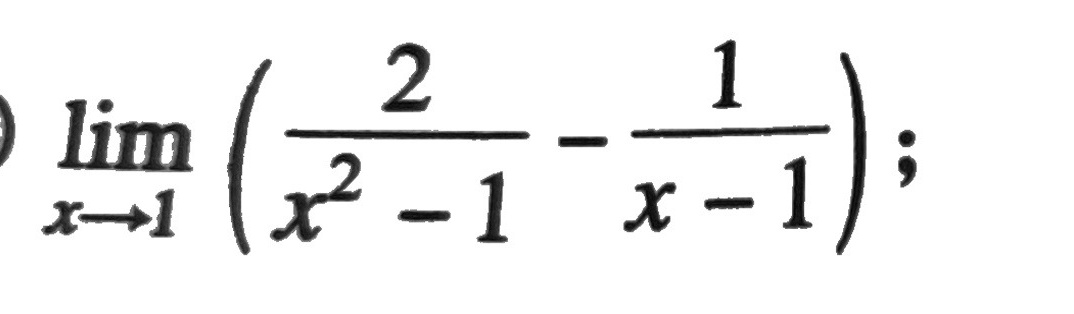
题目解答
答案

解析
考查要点:本题主要考查分式极限的计算,涉及分式的通分、因式分解以及约分等技巧,重点在于处理未定式$\frac{0}{0}$的情况。
解题核心思路:
- 通分合并:将两个分式通分,转化为同一分母的形式,便于合并分子。
- 因式分解:利用平方差公式分解分母,简化表达式。
- 约分化简:通过分子分母的因式分解,约去公共因子,将表达式转化为可直接代入的形式。
破题关键点:
- 识别分母结构:注意到$x^2 -1$可分解为$(x-1)(x+1)$,为后续通分创造条件。
- 符号处理:合并分子时注意符号变化,将$1 - x$转化为$-(x - 1)$,便于约分。
步骤1:通分合并分式
原式为:
$\lim _{x\rightarrow 1}\left(\dfrac {2}{{x}^{2}-1}-\dfrac {1}{x-1}\right)$
将分母$x^2 -1$分解为$(x-1)(x+1)$,并与第二个分式通分:
$\begin{aligned}\text{原式} &= \lim _{x\rightarrow 1} \left( \dfrac{2}{(x-1)(x+1)} - \dfrac{x+1}{(x-1)(x+1)} \right) \\&= \lim _{x\rightarrow 1} \dfrac{2 - (x+1)}{(x-1)(x+1)}.\end{aligned}$
步骤2:化简分子
合并分子:
$2 - (x+1) = 1 - x.$
此时表达式为:
$\lim _{x\rightarrow 1} \dfrac{1 - x}{(x-1)(x+1)}.$
步骤3:因式分解与约分
将分子$1 - x$改写为$-(x - 1)$:
$\dfrac{-(x - 1)}{(x-1)(x+1)} = \dfrac{-1}{x+1}.$
约分后表达式简化为:
$\lim _{x\rightarrow 1} \dfrac{-1}{x+1}.$
步骤4:直接代入求极限
将$x = 1$代入简化后的表达式:
$\dfrac{-1}{1 + 1} = -\dfrac{1}{2}.$