题目
2.已知函数-|||-f(x)= { a,x=0 .-|||-在 x=0 连续,则 a= __ .
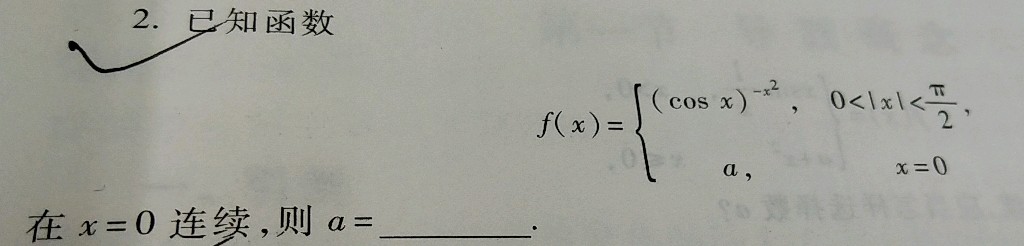
题目解答
答案
解析
考查要点:本题主要考查函数连续性的概念及极限的计算方法,特别是涉及指数函数与三角函数的复合函数极限。
解题核心思路:
函数在某点连续的充要条件是函数在该点的极限值等于函数值。因此,需要计算当$x \to 0$时,$f(x) = (\cos x)^{-x^2}$的极限,并令其等于$a$,从而确定$a$的值。
破题关键点:
- 极限转换:将指数形式转化为自然对数形式,简化计算。
- 泰勒展开:利用$\cos x$的泰勒展开式近似,结合等价无穷小替换,快速求解极限。
步骤1:根据连续性条件列方程
函数$f(x)$在$x=0$处连续,当且仅当:
$\lim_{x \to 0} (\cos x)^{-x^2} = a$
步骤2:对极限取自然对数
设$L = \lim_{x \to 0} (\cos x)^{-x^2}$,则:
$\ln L = \lim_{x \to 0} (-x^2) \cdot \ln (\cos x)$
步骤3:展开$\ln (\cos x)$
当$x \to 0$时,$\cos x \approx 1 - \dfrac{x^2}{2}$,因此:
$\ln (\cos x) \approx \ln \left(1 - \dfrac{x^2}{2}\right) \approx -\dfrac{x^2}{2}$
步骤4:代入并计算极限
将近似式代入$\ln L$:
$\ln L \approx \lim_{x \to 0} (-x^2) \cdot \left(-\dfrac{x^2}{2}\right) = \lim_{x \to 0} \dfrac{x^4}{2} = 0$
步骤5:求原极限值
由$\ln L = 0$得:
$L = e^0 = 1$
结论:
$a = 1$。