题目
(4) lim _(xarrow 0)(({e)^x+x)}^dfrac (1{x)}.
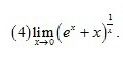
题目解答
答案
最佳答案
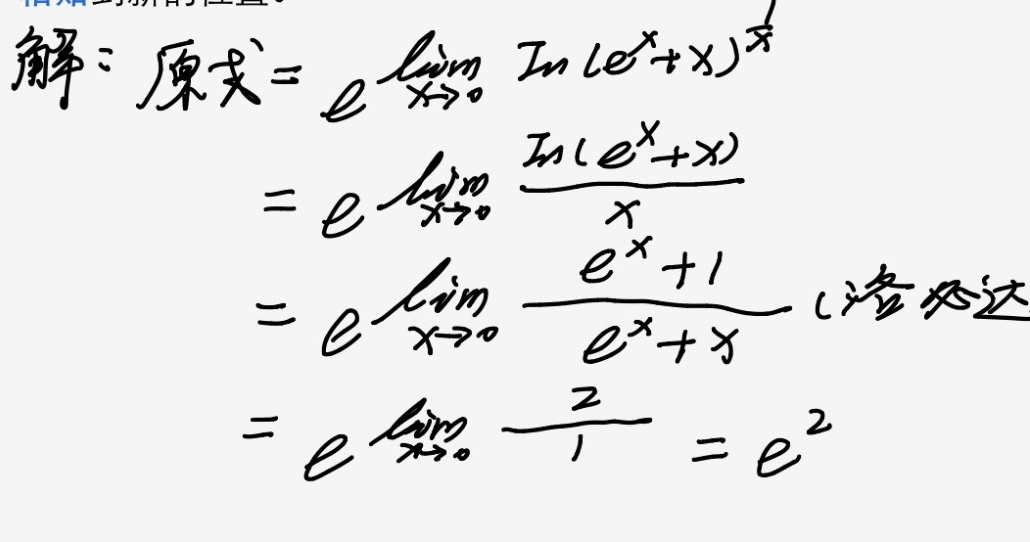
解析
考查要点:本题主要考查极限的计算方法,特别是涉及指数函数与自然对数的复合形式。需要掌握重要极限公式的应用,以及洛必达法则的使用。
解题核心思路:
- 取自然对数将指数形式转化为乘积形式,简化计算。
- 利用等价无穷小替换或洛必达法则求解变形后的极限。
- 最后通过指数运算还原结果。
破题关键点:
- 识别底数为$1 + \text{高阶小量}$的形式,联想到重要极限$\lim_{x \to 0}(1 + kx)^{1/x} = e^k$。
- 正确应用洛必达法则处理$\frac{0}{0}$型不定式。
步骤1:取自然对数
设原式为$L$,则:
$\ln L = \lim_{x \to 0} \frac{\ln(e^x + x)}{x}$
步骤2:应用洛必达法则
当$x \to 0$时,分子$\ln(e^x + x) \to \ln(1 + 0 + 0) = 0$,分母$x \to 0$,属于$\frac{0}{0}$型不定式。对分子分母分别求导:
$\lim_{x \to 0} \frac{\frac{d}{dx}[\ln(e^x + x)]}{\frac{d}{dx}[x]} = \lim_{x \to 0} \frac{\frac{e^x + 1}{e^x + x}}{1}$
步骤3:代入计算
将$x = 0$代入化简后的表达式:
$\frac{e^0 + 1}{e^0 + 0} = \frac{1 + 1}{1 + 0} = 2$
步骤4:还原结果
因此$\ln L = 2$,故$L = e^2$。