题目
甲箱内有 2 个 红球 3 个 白球乙箱内有 2 个 红球 2 个 白球先从甲中任取一球放入乙箱 再从乙箱中任取一球求 ( 1 ) 从乙箱中取出的是红球的 概率 ; ( 2 ) 如果已知从乙箱中取出的是红球的条件下从甲箱中取出的也是红球的概率
甲箱内有 2 个 红球 3 个 白球乙箱内有 2 个 红球 2 个 白球先从甲中任取一球放入乙箱 再从乙箱中任取一球求 ( 1 ) 从乙箱中取出的是红球的 概率 ; ( 2 ) 如果已知从乙箱中取出的是红球的条件下从甲箱中取出的也是红球的概率
题目解答
答案
(1)若从甲箱取出一个红球放到乙箱,则乙箱中有3红球2白球,此时乙箱中取出红球的概率为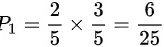
若从甲箱取出一个白球放到乙箱,则乙箱中有2红球3白球,此时乙箱中取出红球的概率为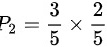
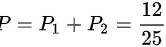
(2)设事件A:从甲箱中取出红球,B:从乙箱中取出红球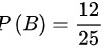 ,
,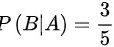
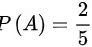
由
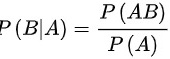 得
得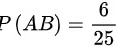
可得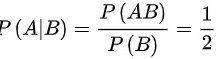
解析
考查要点:本题主要考查全概率公式和贝叶斯公式的应用,涉及条件概率的理解与计算。
解题思路:
- 第(1)问:需要考虑从甲箱取出红球或白球两种情况,分别计算乙箱中红球的概率,再通过全概率公式合并结果。
- 第(2)问:已知乙箱取出红球,求甲箱取出红球的条件概率,需用贝叶斯公式,结合第(1)问的结果进行计算。
关键点:
- 分类讨论甲箱取出球的颜色对乙箱组成的影响。
- 正确应用公式,注意条件概率的转换关系。
第(1)题
情况1:甲箱取出红球
- 概率:甲箱红球占比为 $\dfrac{2}{5}$。
- 乙箱变化:乙箱变为3红2白,共5球。
- 乙箱取红球概率:$\dfrac{3}{5}$。
- 联合概率:$\dfrac{2}{5} \times \dfrac{3}{5} = \dfrac{6}{25}$。
情况2:甲箱取出白球
- 概率:甲箱白球占比为 $\dfrac{3}{5}$。
- 乙箱变化:乙箱变为2红3白,共5球。
- 乙箱取红球概率:$\dfrac{2}{5}$。
- 联合概率:$\dfrac{3}{5} \times \dfrac{2}{5} = \dfrac{6}{25}$。
总概率
将两种情况相加:
$P = \dfrac{6}{25} + \dfrac{6}{25} = \dfrac{12}{25}.$
第(2)题
设事件:
- A:甲箱取出红球。
- B:乙箱取出红球。
根据贝叶斯公式:
$P(A|B) = \dfrac{P(B|A)P(A)}{P(B)}.$
已知:
- $P(B) = \dfrac{12}{25}$(第1问结果)。
- $P(A) = \dfrac{2}{5}$。
- $P(B|A) = \dfrac{3}{5}$(甲取红球后乙箱红球概率)。
计算:
$P(A|B) = \dfrac{\dfrac{3}{5} \times \dfrac{2}{5}}{\dfrac{12}{25}} = \dfrac{\dfrac{6}{25}}{\dfrac{12}{25}} = \dfrac{1}{2}.$