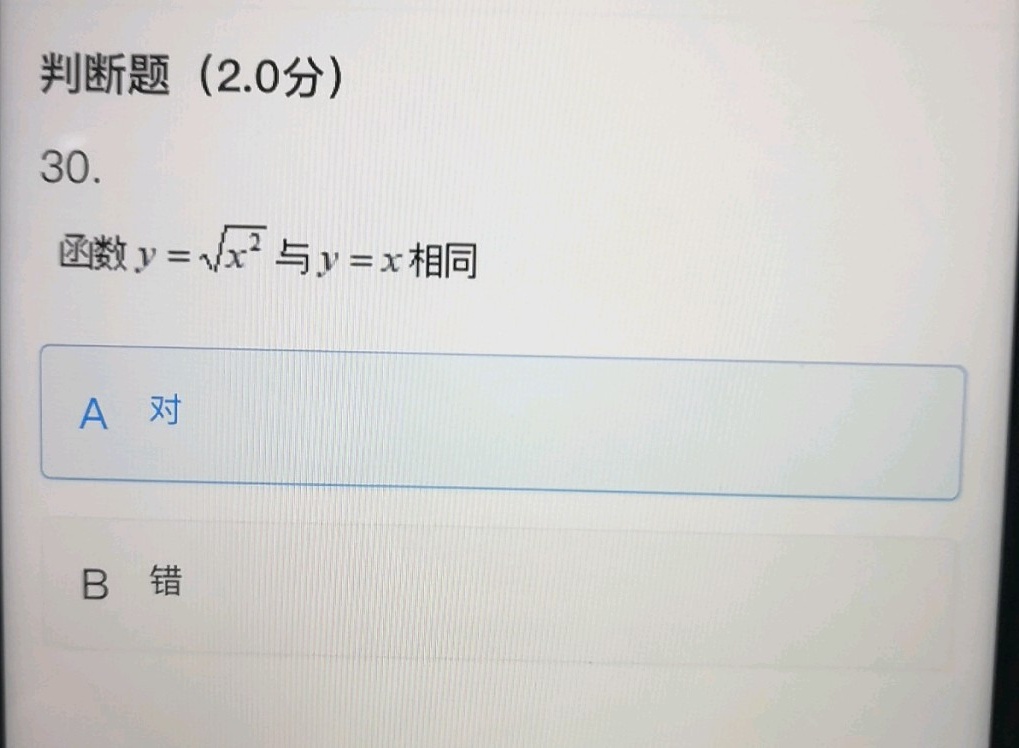
判断题(2.0分)-|||-30.-|||-函数 =sqrt ({x)^2} 与 y=x 相同-|||-A 对-|||-B 错

判断两个函数是否相同，需满足三个条件：定义域相同、对应法则相同、值域相同。
本题中，函数$y=\sqrt{x^2}$与$y=x$的定义域均为全体实数，但对应法则不同：前者等价于$y=|x|$（输出非负），后者直接输出$x$的值。因此，当$x<0$时，两者的函数值不同，且值域也不同（前者值域为$[0,+\infty)$，后者为$(-\infty,+\infty)$）。综上，两者不相同。

函数$y=\sqrt{x^2}$的分析

1. 定义域：$x^2$对所有实数$x$有定义，故定义域为$(-\infty, +\infty)$。
2. 对应法则：$\sqrt{x^2} = |x|$，即输出$x$的绝对值，结果始终非负。
3. 值域：由于$|x| \geq 0$，值域为$[0, +\infty)$。

函数$y=x$的分析

1. 定义域：全体实数，即$(-\infty, +\infty)$。
2. 对应法则：直接输出$x$的值，正负均可。
3. 值域：全体实数，即$(-\infty, +\infty)$。

对比关键点

• 对应法则：当$x<0$时，$y=\sqrt{x^2}=|x|=-x \neq x$，两者输出不同。
• 值域：前者值域为非负实数，后者为全体实数。

结论：两函数不相同，答案为B错。