题目
设常数k>0,函数(x)=ln x-dfrac (x)(e)+k 在 (0,+infty ) 内的零点个数为
设常数k>0,函数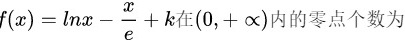
题目解答
答案
要求函数f(x)在区间(0, +∞)内的零点个数,可以分析函数f(x)的性质。
我们可以求函数f(x)的导数来研究其变化情况:
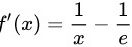
令f'(x)=0,我们可以解得:
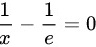
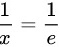
x = e
可以看出,在x=e处,函数f(x)的导数f'(x)发生了变号,即从负数变为正数。根据导数的性质,可以得到以下结论:
1. 当x<e时,f'(x) >0;
2. 当x>e时,f'(x) < 0。
这说明在区间(0, e)内,函数f(x)是单调递减的;而在区间(e, +∞)内,函数f(x)是单调递增的。
再进一步观察函数f(x)在x=e处的取值,我们有:
f(e) = k
这说明在x=e处,函数f(x)的值等于k>0。当x趋近于0时,f(x)<0;当x趋近于正无穷时,f(x)<0。则
根据以上分析,可以得到以下结论:
因此,当常数k>0时,在(0, +∞)内的零点个数为2个。
解析
考查要点:本题主要考查利用导数分析函数的单调性、极值,进而确定函数零点个数的能力。
解题核心思路:
- 求导分析单调性:通过求导找到函数的极值点,确定函数在不同区间的单调性。
- 极值点的函数值:计算极值点处的函数值,结合函数在定义域两端的趋势,判断函数图像与x轴的交点个数。
破题关键点:
- 导数为零的点:解方程$f'(x)=0$得到$x=e$,这是函数的极值点。
- 极值点的函数值:$f(e)=k>0$,说明极值点处函数值为正。
- 函数趋势分析:当$x \to 0^+$和$x \to +\infty$时,$f(x) \to -\infty$,结合极值点的正函数值,可确定零点个数。
-
求导数
函数$f(x)=\ln x - \dfrac{x}{e} + k$的导数为:
$f'(x) = \dfrac{1}{x} - \dfrac{1}{e}.$ -
求极值点
令$f'(x)=0$,解得:
$\dfrac{1}{x} = \dfrac{1}{e} \implies x = e.$
因此,函数在$x=e$处可能取得极值。 -
分析单调性
- 当$x < e$时,$\dfrac{1}{x} > \dfrac{1}{e}$,即$f'(x) > 0$,函数在$(0, e)$上单调递增。
- 当$x > e$时,$\dfrac{1}{x} < \dfrac{1}{e}$,即$f'(x) < 0$,函数在$(e, +\infty)$上单调递减。
- 综上,$x=e$是函数的极大值点。
-
计算极值点的函数值
$f(e) = \ln e - \dfrac{e}{e} + k = 1 - 1 + k = k.$
由于$k > 0$,故$f(e) > 0$。 -
分析函数趋势
- 当$x \to 0^+$时,$\ln x \to -\infty$,而$-\dfrac{x}{e} \to 0$,因此$f(x) \to -\infty$。
- 当$x \to +\infty$时,$\ln x$增长缓慢,而$-\dfrac{x}{e}$主导趋向$-\infty$,因此$f(x) \to -\infty$。
-
确定零点个数
- 在$(0, e)$区间内,函数从$-\infty$递增到$f(e)=k>0$,必存在一个零点。
- 在$(e, +\infty)$区间内,函数从$f(e)=k>0$递减到$-\infty$,必存在一个零点。
- 因此,函数在$(0, +\infty)$内共有2个零点。