题目
设A,B为随机事件,则A,B的充分必要条件是( )A、A,BB、A,BC、A,BD、A,B
设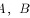 为随机事件,则
为随机事件,则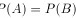 的充分必要条件是( )
的充分必要条件是( )
A、
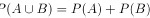
B、
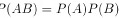
C、
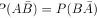
D、
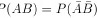
题目解答
答案
C. $P(A\overline {B})=P(B.A)$
解析
考查要点:本题主要考查概率论中事件概率相等的充要条件,涉及事件运算与概率性质的理解。
解题核心思路:
需要找到选项中与$P(A)=P(B)$等价的等式,即该等式成立当且仅当$P(A)=P(B)$。关键在于通过事件运算展开各选项,推导出与$P(A)$和$P(B)$的关系。
破题关键点:
- 选项C通过分解事件$A\overline{B}$和$B\overline{A}$的概率,直接导出$P(A)=P(B)$,且反之亦然,因此是充要条件。
- 其他选项(如独立性、互斥性等)与$P(A)=P(B)$无必然联系。
选项分析
选项C:$P(A\overline{B})=P(B\overline{A})$
-
分解事件概率:
- $P(A\overline{B}) = P(A) - P(AB)$($A$发生但$B$不发生的概率)
- $P(B\overline{A}) = P(B) - P(AB)$($B$发生但$A$不发生的概率)
-
等式变形:
根据题意,$P(A\overline{B}) = P(B\overline{A})$,代入得:
$P(A) - P(AB) = P(B) - P(AB)$
消去$P(AB)$后,直接得到:
$P(A) = P(B)$ -
等价性验证:
- 若$P(A)=P(B)$,则$P(A\overline{B})=P(B\overline{A})$必然成立。
- 反之,若$P(A\overline{B})=P(B\overline{A})$,则必有$P(A)=P(B)$。
因此,选项C是$P(A)=P(B)$的充分必要条件。
其他选项分析
- 选项A:$P(A \cup B) = P(A) + P(B)$
仅当$A$与$B$互斥时成立,与$P(A)=P(B)$无关。 - 选项B:$P(AB) = P(A)P(B)$
表示$A$与$B$独立,独立性与概率相等无必然联系。 - 选项D:$P(AB) = P(\overline{A}B)$
仅说明在$B$发生时,$A$与$\overline{A}$概率相等,与$P(A)=P(B)$无直接关系。