题目
设连续型随机变量服从参数的指数分布,求的概率密度函数。
设连续型随机变量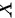 服从参数
服从参数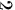 的指数分布,求
的指数分布,求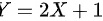 的概率密度函数
的概率密度函数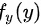 。
。
题目解答
答案
随机变量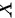 服从参数
服从参数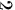 的指数分布,则其密度函数为:
的指数分布,则其密度函数为: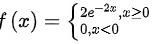
而由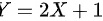 ,设随机变量
,设随机变量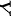 的分布函数为
的分布函数为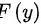 ,
,
当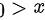 时,即
时,即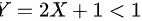 时,
时,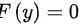
当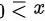 时,即
时,即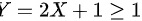 时,
时,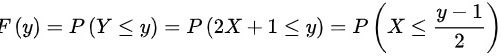
因此,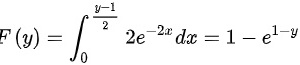
而由此,对应的密度函数即为:
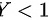 时,
时,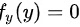 ;
;
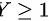 时,
时,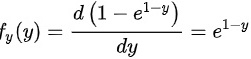 ;
;
综上,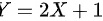 的概率密度函数
的概率密度函数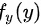 为
为
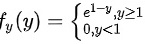
解析
步骤 1:确定随机变量X的概率密度函数
随机变量X服从参数为λ的指数分布,其概率密度函数为:
\[ f(x) = \lambda e^{-\lambda x} \]
其中,x ≥ 0。
步骤 2:确定随机变量Y的分布函数
由Y = 2X + 1,设随机变量Y的分布函数为F(y)。
当y < 1时,即2X + 1 < 1,即X < 0,此时F(y) = 0。
当y ≥ 1时,即2X + 1 ≥ 1,即X ≥ 0,此时F(y) = P(X ≤ (y - 1)/2)。
因此,F(y) = ∫_{0}^{(y-1)/2} λe^{-λx} dx = 1 - e^{-λ(y-1)/2}。
步骤 3:确定随机变量Y的概率密度函数
由F(y)的表达式,对F(y)求导得到Y的概率密度函数f(y)。
当y < 1时,f(y) = 0。
当y ≥ 1时,f(y) = dF(y)/dy = (λ/2)e^{-λ(y-1)/2}。
随机变量X服从参数为λ的指数分布,其概率密度函数为:
\[ f(x) = \lambda e^{-\lambda x} \]
其中,x ≥ 0。
步骤 2:确定随机变量Y的分布函数
由Y = 2X + 1,设随机变量Y的分布函数为F(y)。
当y < 1时,即2X + 1 < 1,即X < 0,此时F(y) = 0。
当y ≥ 1时,即2X + 1 ≥ 1,即X ≥ 0,此时F(y) = P(X ≤ (y - 1)/2)。
因此,F(y) = ∫_{0}^{(y-1)/2} λe^{-λx} dx = 1 - e^{-λ(y-1)/2}。
步骤 3:确定随机变量Y的概率密度函数
由F(y)的表达式,对F(y)求导得到Y的概率密度函数f(y)。
当y < 1时,f(y) = 0。
当y ≥ 1时,f(y) = dF(y)/dy = (λ/2)e^{-λ(y-1)/2}。