题目
设微分方程^11+4y'+ay=(e)^-2x的特解形式是^11+4y'+ay=(e)^-2x,则^11+4y'+ay=(e)^-2x( )
设微分方程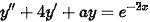 的特解形式是
的特解形式是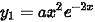 ,则
,则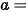 ( )
( )
题目解答
答案
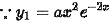
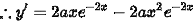
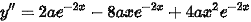
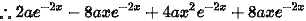
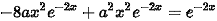
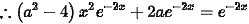
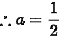
解析
步骤 1:计算${y}_{1}$的一阶导数
给定${y}_{1}=a{x}^{2}{e}^{-2x}$,我们首先计算其一阶导数$y'$。
$y'=2ax{e}^{-2x}-2a{x}^{2}{e}^{-2x}$
步骤 2:计算${y}_{1}$的二阶导数
接下来,我们计算${y}_{1}$的二阶导数$y''$。
$y''=2a{e}^{-2x}-8ax{e}^{-2x}+4a{x}^{2}{e}^{-2x}$
步骤 3:将$y''$、$y'$和$y$代入原微分方程
将$y''$、$y'$和$y$代入原微分方程${y}^{11}+4y'+ay={e}^{-2x}$,得到:
$2a{e}^{-2x}-8ax{e}^{-2x}+4a{x}^{2}{e}^{-2x}+8ax{e}^{-2x}-8a{x}^{2}{e}^{-2x}+{a}^{2}{x}^{2}{e}^{-2x}={e}^{-2x}$
化简得:
$({a}^{2}-4){x}^{2}{e}^{-2x}+2a{e}^{-2x}={e}^{-2x}$
步骤 4:求解$a$
由于${e}^{-2x}$不为零,我们可以将方程两边同时除以${e}^{-2x}$,得到:
$({a}^{2}-4){x}^{2}+2a=1$
由于${x}^{2}$的系数必须为零,以保证方程对所有$x$都成立,我们得到:
${a}^{2}-4=0$
解得$a=\pm2$,但考虑到$2a=1$,我们得到$a=\dfrac{1}{2}$。
给定${y}_{1}=a{x}^{2}{e}^{-2x}$,我们首先计算其一阶导数$y'$。
$y'=2ax{e}^{-2x}-2a{x}^{2}{e}^{-2x}$
步骤 2:计算${y}_{1}$的二阶导数
接下来,我们计算${y}_{1}$的二阶导数$y''$。
$y''=2a{e}^{-2x}-8ax{e}^{-2x}+4a{x}^{2}{e}^{-2x}$
步骤 3:将$y''$、$y'$和$y$代入原微分方程
将$y''$、$y'$和$y$代入原微分方程${y}^{11}+4y'+ay={e}^{-2x}$,得到:
$2a{e}^{-2x}-8ax{e}^{-2x}+4a{x}^{2}{e}^{-2x}+8ax{e}^{-2x}-8a{x}^{2}{e}^{-2x}+{a}^{2}{x}^{2}{e}^{-2x}={e}^{-2x}$
化简得:
$({a}^{2}-4){x}^{2}{e}^{-2x}+2a{e}^{-2x}={e}^{-2x}$
步骤 4:求解$a$
由于${e}^{-2x}$不为零,我们可以将方程两边同时除以${e}^{-2x}$,得到:
$({a}^{2}-4){x}^{2}+2a=1$
由于${x}^{2}$的系数必须为零,以保证方程对所有$x$都成立,我们得到:
${a}^{2}-4=0$
解得$a=\pm2$,但考虑到$2a=1$,我们得到$a=\dfrac{1}{2}$。