题目
(x)f在(x)f邻域内有定义,以下命题正确的是:① 如果 (x)f 在 (x)f 处可导,那么有(x)f;② (x)f 存在,则(x)f在(x)f处可导;③(x)f,则(x)f;④(x)f存在是(x)f在(x)f可导的充分不必要条件。(A)①②(B)①③(C)③②(D)③④
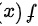 在
在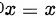 邻域内有定义,以下命题正确的是:
邻域内有定义,以下命题正确的是:
① 如果 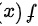 在
在 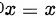 处可导,那么有
处可导,那么有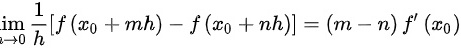 ;
;
② 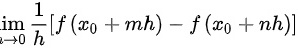 存在,则
存在,则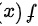 在
在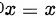 处可导;
处可导;
③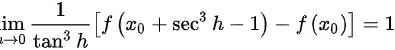 ,则
,则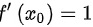 ;
;
④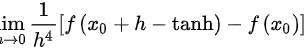 存在是
存在是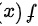 在
在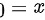 可导的充分不必要条件。
可导的充分不必要条件。
(A)①②
(B)①③
(C)③②
(D)③④
题目解答
答案
解:
结合【思路点拨】中导数、导函数的定义,对①到④逐个分析:
① 如果 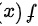 在
在 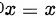 处可导,结合【思路点拨】中导函数的定义,那么有
处可导,结合【思路点拨】中导函数的定义,那么有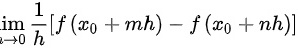
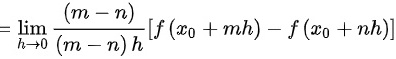
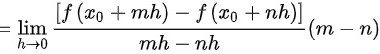
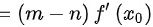 ,因此①正确。
,因此①正确。
② 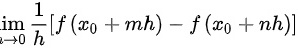 存在,则
存在,则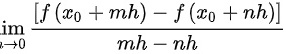 存在,由【思路点拨】中导函数的定义知
存在,由【思路点拨】中导函数的定义知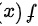 在
在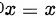 处可导,因此②正确。
处可导,因此②正确。
③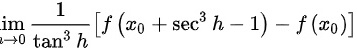
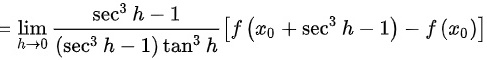
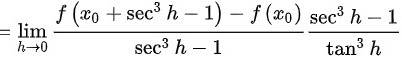
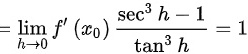 ,利用反证法,若
,利用反证法,若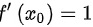 ,则有
,则有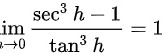 ,不成立!因此③错误。
,不成立!因此③错误。
④所给极限式子是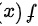 在
在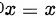 处有关的极限,与
处有关的极限,与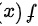 在
在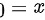 是否可导没有直接联系,因此④错误。
是否可导没有直接联系,因此④错误。
综上,①②正确,③④错误。
故,答案选A。