题目
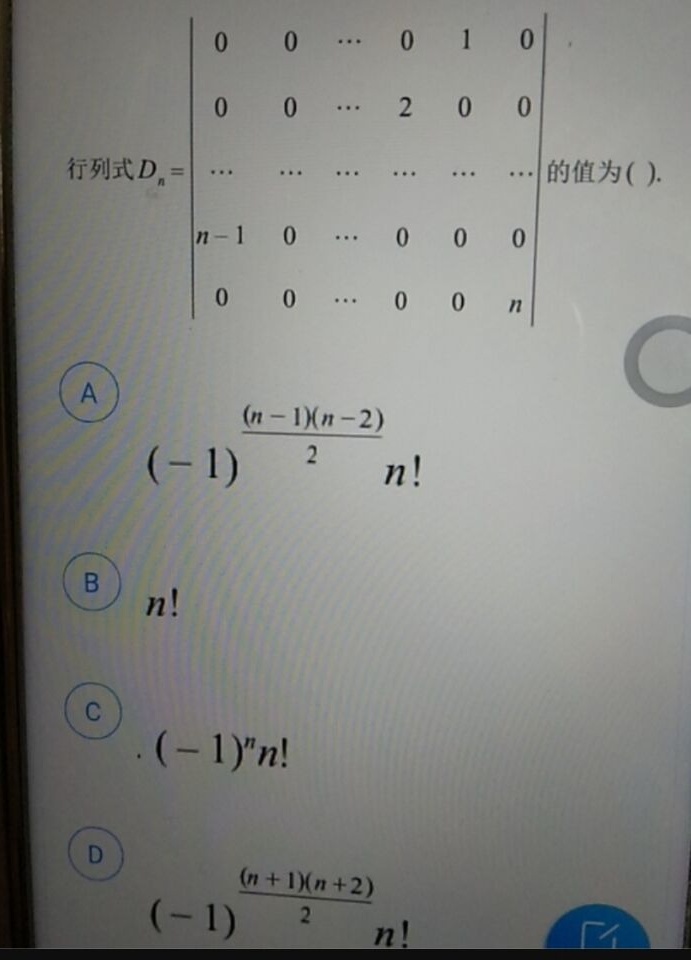
0 0 ...0 1 0-|||-0 0 ...2 0 0-|||-行列式 _(n)= ........ 的值为 .-|||-n-1 0 ...0 0 0-|||-0 0 ...0 0 n-|||-A ((-1))^dfrac ((n-1)(n-2){2)n!}!-|||-B n!-|||-C-|||-((-1))^nn!!-|||-D (-1)dfrac ((n+1)(n+2))(2)n
题目解答
答案

解析
步骤 1:观察行列式结构
观察行列式 ${D}_{n}$ 的结构,可以看到它是一个上三角行列式,除了主对角线上的元素外,其余元素均为0。主对角线上的元素依次为:$2, 3, 4, ..., n-1, n$。
步骤 2:计算行列式的值
上三角行列式的值等于主对角线上元素的乘积。因此,行列式 ${D}_{n}$ 的值为:$2 \times 3 \times 4 \times ... \times (n-1) \times n$。这可以表示为 $n!$,但需要考虑行列式中负号的影响。
步骤 3:考虑行列式中负号的影响
行列式中负号的影响取决于主对角线上元素的排列。由于主对角线上的元素是从2开始的,因此需要考虑从2到n的排列中负号的个数。排列中负号的个数为 $\dfrac{(n-1)(n-2)}{2}$,因此行列式的值为 ${(-1)}^{\dfrac{(n-1)(n-2)}{2}}n!$。
观察行列式 ${D}_{n}$ 的结构,可以看到它是一个上三角行列式,除了主对角线上的元素外,其余元素均为0。主对角线上的元素依次为:$2, 3, 4, ..., n-1, n$。
步骤 2:计算行列式的值
上三角行列式的值等于主对角线上元素的乘积。因此,行列式 ${D}_{n}$ 的值为:$2 \times 3 \times 4 \times ... \times (n-1) \times n$。这可以表示为 $n!$,但需要考虑行列式中负号的影响。
步骤 3:考虑行列式中负号的影响
行列式中负号的影响取决于主对角线上元素的排列。由于主对角线上的元素是从2开始的,因此需要考虑从2到n的排列中负号的个数。排列中负号的个数为 $\dfrac{(n-1)(n-2)}{2}$,因此行列式的值为 ${(-1)}^{\dfrac{(n-1)(n-2)}{2}}n!$。