4.设 =(x)^2+(y)^2, 其中 y=f(x) 为由方程 ^2-xy+(y)^2=1 所确定的隐函-|||-数,求 dx/(dx) 及 dfrac ({d)^2z}(d{x)^2}

题目解答
答案
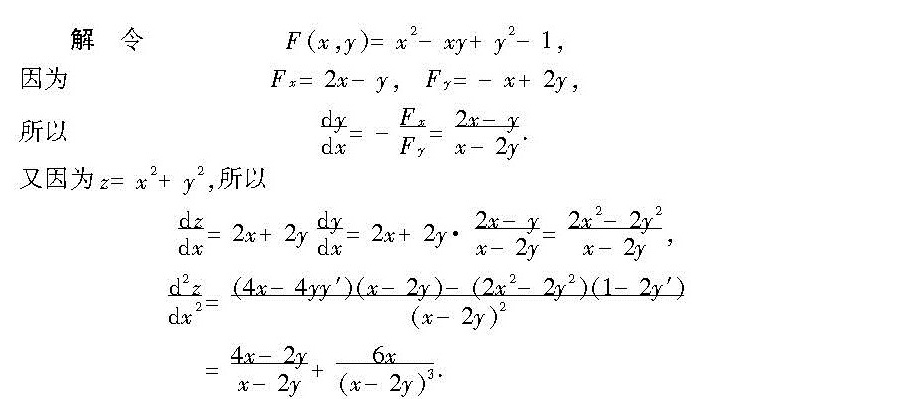
解析
考查要点:本题主要考查隐函数求导及复合函数求导法则的应用,涉及一阶导数和二阶导数的计算。
解题核心思路:
- 隐函数求导:利用隐函数定理对给定方程求导,得到$\dfrac{dy}{dx}$。
- 链式法则:对$z = x^2 + y^2$求导时,需将$y$视为$x$的函数,应用链式法则。
- 商的导数法则:在计算二阶导数时,需对分式形式的$\dfrac{dz}{dx}$再次求导。
破题关键点:
- 正确求出$\dfrac{dy}{dx}$:通过隐函数定理,明确偏导数$F_x$和$F_y$的计算。
- 代数化简:在求导过程中,注意分子分母的展开与合并同类项,避免计算错误。
1. 求$\dfrac{dy}{dx}$
令$F(x, y) = x^2 - xy + y^2 - 1 = 0$,根据隐函数定理:
$\dfrac{dy}{dx} = -\dfrac{F_x}{F_y} = -\dfrac{2x - y}{-x + 2y} = \dfrac{2x - y}{x - 2y}.$
2. 求$\dfrac{dz}{dx}$
由$z = x^2 + y^2$,应用链式法则:
$\dfrac{dz}{dx} = 2x + 2y \cdot \dfrac{dy}{dx}.$
将$\dfrac{dy}{dx}$代入:
$\dfrac{dz}{dx} = 2x + 2y \cdot \dfrac{2x - y}{x - 2y} = \dfrac{2x(x - 2y) + 2y(2x - y)}{x - 2y} = \dfrac{2x^2 - 2y^2}{x - 2y}.$
3. 求$\dfrac{d^2z}{dx^2}$
对$\dfrac{dz}{dx} = \dfrac{2x^2 - 2y^2}{x - 2y}$应用商的导数法则:
$\dfrac{d^2z}{dx^2} = \dfrac{(4x - 4y \cdot \dfrac{dy}{dx})(x - 2y) - (2x^2 - 2y^2)(1 - 2\dfrac{dy}{dx})}{(x - 2y)^2}.$
展开并代入$\dfrac{dy}{dx} = \dfrac{2x - y}{x - 2y}$,化简后得:
$\dfrac{d^2z}{dx^2} = \dfrac{4x - 2y}{x - 2y} + \dfrac{6x}{(x - 2y)^3}.$