题目
函数=4((x+2))^2+3的单调增加区间是（）
函数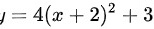
的单调增加区间是（）
题目解答
答案
对于函数
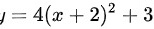
对其求导得
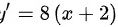
令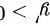
得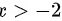
当其导数大于零时，函数单调增加
即函数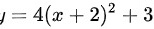的单调增加区间是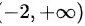
解析
步骤 1：求导
对函数$y=4{(x+2)}^{2}+3$求导，得到$y'=8(x+2)$。
步骤 2：确定导数大于零的区间
令$y'\gt 0$，即$8(x+2)\gt 0$，解得$x\gt -2$。
步骤 3：确定单调增加区间
当导数大于零时，函数单调增加，因此函数$y=4{(x+2)}^{2}+3$的单调增加区间是$(-2,+\infty )$。
对函数$y=4{(x+2)}^{2}+3$求导，得到$y'=8(x+2)$。
步骤 2：确定导数大于零的区间
令$y'\gt 0$，即$8(x+2)\gt 0$，解得$x\gt -2$。
步骤 3：确定单调增加区间
当导数大于零时，函数单调增加，因此函数$y=4{(x+2)}^{2}+3$的单调增加区间是$(-2,+\infty )$。