如图①,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.(1)如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.(2)如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC,DE⊥AB,且BE=a,求AB-AC的值.(用含a的代数式表示)C-|||-C D-|||-D C D-|||-A B A B A E B-|||-图① 图② 图③
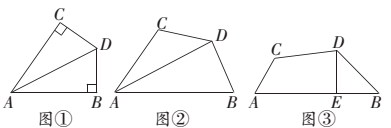
如图①,AD平分∠BAC.∠B+∠C=180°,∠B=90°,易知:DB=DC.
(1)如图②,AD平分∠BAC,∠ABD+∠ACD=180°,∠ABD<90°,求证:DB=DC.
(2)如图③,在四边形ABDC中,∠B=45°,∠C=135°,DB=DC,DE⊥AB,且BE=a,求AB-AC的值.(用含a的代数式表示)
题目解答
答案
(1)证明:如图,作DE⊥AB于E,DF⊥AC于F,
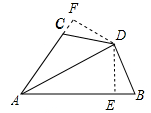
∵DA平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF.
角平分线上的点到两边的距离相等
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
同角(等角)的补角相等
在△DFC和△DEB中,
⎧⎪⎨⎪⎩∠F=∠DEB=90°∠FCD=∠BDF=DB,
∴△DFC≌△DEB,
全等三角形的判定(AAS)
∴DC=DB.
全等三角形的性质
(2)解:如图,连接AD,作DE⊥AB于E,DF⊥AC于F.
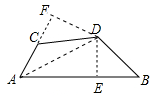
∵∠B+∠ACD=180°,∠ACD+∠FCD=180°,
∴∠B=∠FCD.
同角(等角)的补角相等
在△DFC和△DEB中,
⎧⎪⎨⎪⎩∠F=∠DEB=90°∠FCD=∠BDC=DB,
∴△DFC≌△DEB,
全等三角形的判定(AAS)
∴DF=DE,CF=BE,
全等三角形的性质
在Rt△ADF和Rt△ADE中,
{AD=ADDE=DF,
HL定理
∴△ADF≌△ADE,
∴AF=AE,
全等三角形的性质
∴AB-AC=(AE+BE)-(AF-CF)=AE+BE-AF+CF=BE+CF=2BE=2a.
解析
考查要点:本题主要考查角平分线的性质、全等三角形的判定与性质、垂直关系的应用,以及代数式的几何意义转化。
解题思路:
- 第(1)题:通过构造垂直辅助线,利用角平分线性质得到相等的高,结合补角关系证明三角形全等,从而得到边相等。
- 第(2)题:通过连接对角线构造全等三角形,结合垂直关系和勾股定理,将线段差转化为已知量的代数表达。
破题关键:
- 角平分线+垂直⇒距离相等(第1题核心)
- 补角相等⇒角度转化(全等条件的关键)
- 线段差拆分⇒利用对称性简化表达(第2题核心)
第(1)题
作垂直辅助线
作$DE \perp AB$于$E$,$DF \perp AC$于$F$,利用角平分线性质得$DE=DF$。
角度转化
由$\angle ABD + \angle ACD = 180^\circ$,结合$\angle ACD + \angle FCD = 180^\circ$,得$\angle ABD = \angle FCD$。
证明三角形全等
在$\triangle DFC$与$\triangle DEB$中:
- $\angle F = \angle DEB = 90^\circ$(垂直)
- $\angle FCD = \angle ABD$(已证)
- $DF = DE$(角平分线性质)
由AAS判定得$\triangle DFC \cong \triangle DEB$,故$DC = DB$。
第(2)题
连接对角线并作垂线
连接$AD$,作$DE \perp AB$于$E$,$DF \perp AC$于$F$,同理得$DE=DF$。
全等三角形性质
由$\triangle DFC \cong \triangle DEB$得$CF = BE = a$,且$\triangle ADF \cong \triangle ADE$(HL),故$AF = AE$。
线段差转化
$\begin{aligned}AB - AC &= (AE + BE) - (AF - CF) \\&= AE + BE - AF + CF \\&= BE + CF \quad (\because AF = AE) \\&= a + a = 2a\end{aligned}$