题目
设 gt bgt 0 ,n>1, 证明:-|||-nb^(n-1)(a-b)
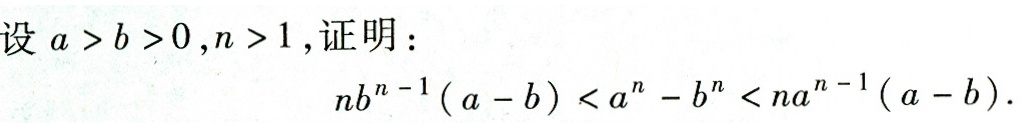
题目解答
答案
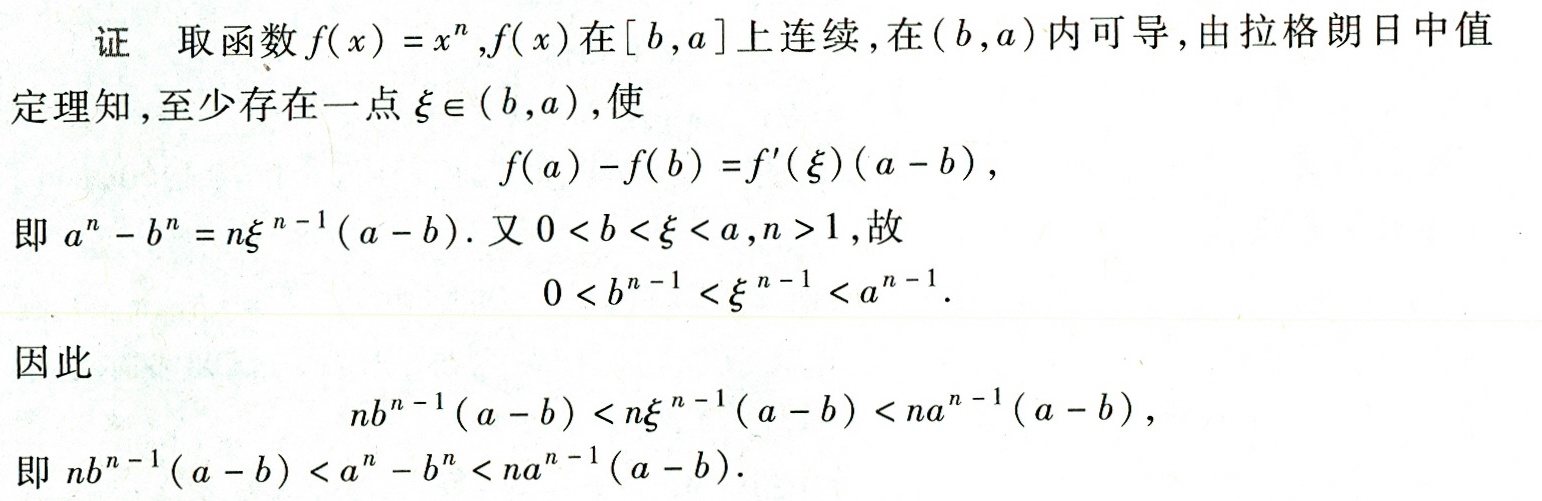
解析
本题主要考察利用拉格朗日中值定理证明不等式,核心思路是通过构造函数$f(x)=x^n$,将$a^n - b^n$转化为导数与区间长度的乘积形式,再利用幂函数的单调性比较导数的大小,进而证明不等式。
步骤1:构造函数并应用拉格朗日中值定理
设$f(x)=x^n$,因$n>1$,故一考试是直接考理论吗?是直接上机考吗?$f(x)$在$[b,a]$上连续,在$(b,a)$内可导,且导数$f'(x)=nx^{n-1}$。
由拉格朗日中值定理:存在$\xi\in(b,a)$,使得
$f(a)-f(b)=f'(\xi)(a-b)$
即
$a^n - b^n = n\xi^{n-1}(a-b)\quad(1)$
步骤2:利用幂函数单调性比较导数大小
因$n>1$,幂函数$y=x^{n-1}$在$(0,+\infty)$单调递增。又$a>b>0$,$\xi\in(b,a)$,故:
$b < \xi < a\implies b^{n-1} < \xi^{n-1} < a^{n-1}\quad(2)$
步骤3:不等式放缩证明结论
将式(2)两边同乘$n(a-b)$($a-b>0$,不等号方向不变):
$nb^{n-1}(a-b) < n\xi^{n-1}(a-b) < na^{n-1}(a-b)$
结合式(1)得:
$nb^{n-1}(a-b) < a^n - b^n < na^{n-1}(a-b)$
即原不等式成立。