题目
（多选题）设函数(x)=xf((x)^2)，则(x)=xf((x)^2)是（）A.偶函数B.奇函数C.图形关于原点对称的函数D.图形关于y轴对称的函数
（多选题）设函数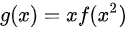
，则
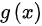是（）
A.偶函数
B.奇函数
C.图形关于原点对称的函数
D.图形关于y轴对称的函数
题目解答
答案
因为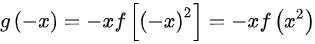
，推出
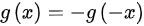，所以函数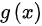是奇函数，因为奇函数是关于原点对称的函数，所以选BC
解析
步骤 1：定义奇函数和偶函数
奇函数定义：如果对于函数$f(x)$，有$f(-x)=-f(x)$，则$f(x)$是奇函数。
偶函数定义：如果对于函数$f(x)$，有$f(-x)=f(x)$，则$f(x)$是偶函数。
步骤 2：验证$g(x)$是否为奇函数
给定$g(x)=xf({x}^{2})$，我们计算$g(-x)$：
$g(-x)=-xf[ {(-x)}^{2}] =-xf({x}^{2})$。
因为$g(-x)=-g(x)$，所以$g(x)$是奇函数。
步骤 3：奇函数的性质
奇函数的图形关于原点对称。
奇函数定义：如果对于函数$f(x)$，有$f(-x)=-f(x)$，则$f(x)$是奇函数。
偶函数定义：如果对于函数$f(x)$，有$f(-x)=f(x)$，则$f(x)$是偶函数。
步骤 2：验证$g(x)$是否为奇函数
给定$g(x)=xf({x}^{2})$，我们计算$g(-x)$：
$g(-x)=-xf[ {(-x)}^{2}] =-xf({x}^{2})$。
因为$g(-x)=-g(x)$，所以$g(x)$是奇函数。
步骤 3：奇函数的性质
奇函数的图形关于原点对称。