题目
下列微分方程中是二阶微分方程的是（ ）（A）((y'))^2+4y-3x=0（B）((y'))^2+4y-3x=0（C）((y'))^2+4y-3x=0（D）((y'))^2+4y-3x=0
下列微分方程中是二阶微分方程的是（ ）
（A）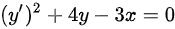
（B）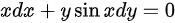
（C）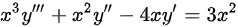
（D）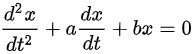
题目解答
答案
解：对选项A，
∵微分方程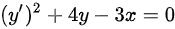为导数形式微分方程且最高阶导数为一阶
∴微分方程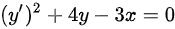为一阶微分方程
∴选项A错误
对选项B，
由微分方程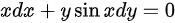可得：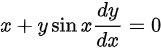
∴微分方程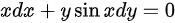为微分形式的微分方程且最高阶微分为一阶
∴微分方程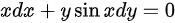为一阶微分方程
∴选项B错误
对选项C，
∵微分方程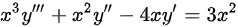为导数形式的微分方程且最高阶导数为三阶
∴微分方程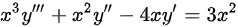为三阶微分方程
∴选项C错误
对选项D，
∵微分方程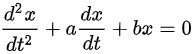为微分形式的微分方程且最高阶微分为二阶
∴微分方程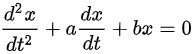为二阶微分方程
∴选项D正确
故正确答案为选项D
解析
步骤 1：分析选项A
微分方程${(y')}^{2}+4y-3x=0$为导数形式微分方程且最高阶导数为一阶，因此为一阶微分方程。
步骤 2：分析选项B
微分方程$xdx+y\sin xdy=0$可写为$x+y\sin x\dfrac {dy}{dx}=0$，为微分形式的微分方程且最高阶微分为一阶，因此为一阶微分方程。
步骤 3：分析选项C
微分方程${x}^{3}{y}^{111}+{x}^{2}{y}^{11}-4xy'=3{x}^{2}$为导数形式的微分方程且最高阶导数为三阶，因此为三阶微分方程。
步骤 4：分析选项D
微分方程$\dfrac {{d}^{2}x}{d{t}^{2}}+a\dfrac {dx}{dt}+bx=0$为微分形式的微分方程且最高阶微分为二阶，因此为二阶微分方程。
微分方程${(y')}^{2}+4y-3x=0$为导数形式微分方程且最高阶导数为一阶，因此为一阶微分方程。
步骤 2：分析选项B
微分方程$xdx+y\sin xdy=0$可写为$x+y\sin x\dfrac {dy}{dx}=0$，为微分形式的微分方程且最高阶微分为一阶，因此为一阶微分方程。
步骤 3：分析选项C
微分方程${x}^{3}{y}^{111}+{x}^{2}{y}^{11}-4xy'=3{x}^{2}$为导数形式的微分方程且最高阶导数为三阶，因此为三阶微分方程。
步骤 4：分析选项D
微分方程$\dfrac {{d}^{2}x}{d{t}^{2}}+a\dfrac {dx}{dt}+bx=0$为微分形式的微分方程且最高阶微分为二阶，因此为二阶微分方程。