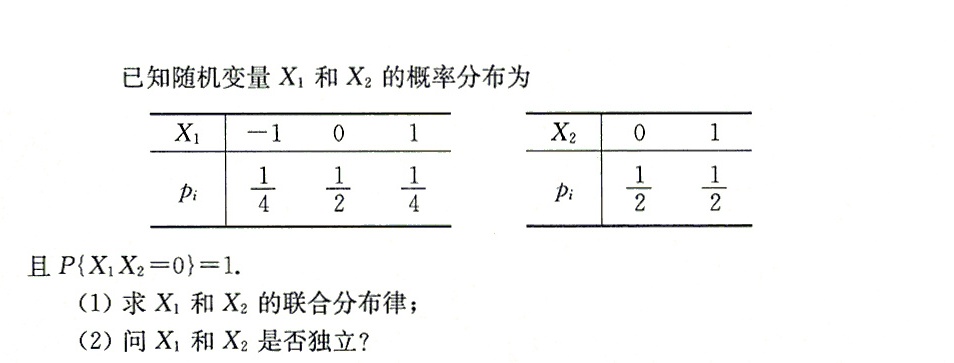
已知随机变量X1和X2的概率分布为-|||-X1 -1 0 1 X2 0 1-|||-pi dfrac (1)(4) .dfrac (1)(2) dfrac (1)(4) pi .dfrac (1)(2) dfrac (1)(2)-|||-且 {X)_(1)(X)_(2)=0} =1 。-|||-(1)求X1和X2的联合分布律;-|||-(2)问X1和X2是否独立?

步骤 1：确定边缘分布律
根据题目给出的边缘分布律，我们有：
- 对于X1，$P\{X_1=-1\} = \dfrac{1}{4}$，$P\{X_1=0\} = \dfrac{1}{2}$，$P\{X_1=1\} = \dfrac{1}{4}$。
- 对于X2，$P\{X_2=0\} = \dfrac{1}{2}$，$P\{X_2=1\} = \dfrac{1}{2}$。

步骤 2：利用条件 $P\{X_1X_2=0\} = 1$ 求联合分布律
由于 $P\{X_1X_2=0\} = 1$，这意味着 $X_1$ 和 $X_2$ 不能同时取非零值。因此，$P\{X_1=1, X_2=1\} = 0$，$P\{X_1=-1, X_2=1\} = 0$。根据边缘分布律，我们可以求出其他联合概率：
- $P\{X_1=-1, X_2=0\} = P\{X_1=-1\} - P\{X_1=-1, X_2=1\} = \dfrac{1}{4} - 0 = \dfrac{1}{4}$。
- $P\{X_1=0, X_2=0\} = P\{X_2=0\} - P\{X_1=1, X_2=0\} - P\{X_1=-1, X_2=0\} = \dfrac{1}{2} - 0 - \dfrac{1}{4} = \dfrac{1}{4}$。
- $P\{X_1=0, X_2=1\} = P\{X_2=1\} - P\{X_1=1, X_2=1\} - P\{X_1=-1, X_2=1\} = \dfrac{1}{2} - 0 - 0 = \dfrac{1}{2}$。
- $P\{X_1=1, X_2=0\} = P\{X_1=1\} - P\{X_1=1, X_2=1\} = \dfrac{1}{4} - 0 = \dfrac{1}{4}$。

步骤 3：判断X1和X2是否独立
两个随机变量X1和X2独立的充分必要条件是对于所有可能的值i和j，有$P\{X_1=i, X_2=j\} = P\{X_1=i\} \cdot P\{X_2=j\}$。根据我们求出的联合分布律，我们可以验证：
- $P\{X_1=-1, X_2=0\} = \dfrac{1}{4} \neq P\{X_1=-1\} \cdot P\{X_2=0\} = \dfrac{1}{4} \cdot \dfrac{1}{2} = \dfrac{1}{8}$。
因此，X1和X2不独立。