题目
已知 y1=e 3x -x(e)^2x, y1=e 3x -x(e)^2x, y1=e 3x -x(e)^2x是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件 y1=e 3x -x(e)^2x的解为y= ________ .
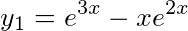 ,
,
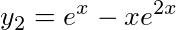 ,
,
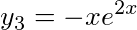 是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件
是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件
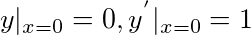 的解为y= ________ .
的解为y= ________ .
题目解答
答案
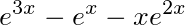
解析
考查要点:本题主要考查二阶常系数非齐次线性微分方程的解的结构,以及利用初始条件确定特解的能力。
解题核心思路:
- 确定齐次方程的解:通过已知的三个非齐次方程解,计算它们的差,得到齐次方程的两个线性无关解。
- 构造通解:通解为齐次方程的通解加上非齐次方程的一个特解。
- 代入初始条件:通过初始条件确定通解中的待定常数,得到满足条件的特解。
破题关键点:
- 差解法:利用非齐次方程解的差属于齐次方程解的性质,找到齐次方程的两个线性无关解。
- 特征方程:通过齐次方程的解形式(指数函数)反推特征方程,确定微分方程的形式。
- 特解构造:结合非齐次项的形式,确定特解的结构。
步骤1:确定齐次方程的解
计算非齐次方程解的差:
- $y_1 - y_2 = e^{3x} - e^x$
- $y_2 - y_3 = e^x$
由此可知,齐次方程的两个线性无关解为 $e^{3x}$ 和 $e^x$,对应的特征方程为 $(r-3)(r-1)=0$,即 $r^2 -4r +3=0$。
步骤2:构造通解
非齐次方程的通解为:
$y = C_1 e^{3x} + C_2 e^{x} + \text{特解}$
观察已知解的结构,特解可取 $-x e^{2x}$(因非齐次项为 $x e^{2x}$,且特征根不含2)。
步骤3:代入初始条件
通解形式为:
$y = C_1 e^{3x} + C_2 e^{x} - x e^{2x}$
代入初始条件:
- $y(0)=0$:
$C_1 + C_2 = 0$ - $y'(0)=1$:
求导得:
$y' = 3C_1 e^{3x} + C_2 e^{x} - e^{2x} - 2x e^{2x}$
代入$x=0$:
$3C_1 + C_2 - 1 = 1 \quad \Rightarrow \quad 3C_1 + C_2 = 2$
步骤4:解方程组
联立方程:
$\begin{cases}C_1 + C_2 = 0 \\3C_1 + C_2 = 2\end{cases}$
解得 $C_1 = 1$,$C_2 = -1$。