题目
设A为5阶矩阵，A的秩5，则矩阵A×的秩A×__________
设A为5阶矩阵，A的秩5，则矩阵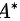
的秩
__________
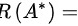题目解答
答案
当r(A)=n时，由于公式r(AB)<=r(A),r(AB)<=r(B)，并且r(AA*)=r(I)=n,则，伴随的秩为n，∵A为5阶矩阵，A的秩5，∴矩阵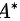的秩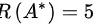
。
故答案为5。
解析
步骤 1：理解伴随矩阵的性质
伴随矩阵$A^*$的秩与原矩阵$A$的秩有直接关系。当$A$的秩为$n$时，$A^*$的秩也为$n$。这是因为$A$的秩为$n$意味着$A$是满秩的，即$A$是可逆的，从而$A^*$也是满秩的。
步骤 2：应用伴随矩阵的性质
由于题目中给出$A$为5阶矩阵，且$A$的秩为5，即$A$是满秩的，因此$A^*$也是满秩的。所以$A^*$的秩也是5。
伴随矩阵$A^*$的秩与原矩阵$A$的秩有直接关系。当$A$的秩为$n$时，$A^*$的秩也为$n$。这是因为$A$的秩为$n$意味着$A$是满秩的，即$A$是可逆的，从而$A^*$也是满秩的。
步骤 2：应用伴随矩阵的性质
由于题目中给出$A$为5阶矩阵，且$A$的秩为5，即$A$是满秩的，因此$A^*$也是满秩的。所以$A^*$的秩也是5。