1.计算下列极限:-|||-(1) lim _(xarrow 2)dfrac ({x)^2+5}(x-3) .-|||-(3) lim _(xarrow 1)dfrac ({x)^2-2x+1}({x)^2-1}-|||-(5) lim _(harrow 0)dfrac ({(x+h))^2-(x)^2}(h) :-|||-(7) lim _(xarrow infty )dfrac ({x)^2-1}(2{x)^2-x-1} ;-|||-(9) lim _(xarrow a)dfrac ({x)^2-6x+8}({x)^2-5x+4} =-|||-(11) lim _(narrow infty )(1+dfrac (1)(2)+dfrac (1)(4)+... +dfrac (1)({2)^n})-|||-1/2^n);(12)-|||-(13) lim _(narrow infty )dfrac ((n+1)(n+2)(n+3))(5{n)^2} ;-|||-(2) lim _(xarrow sqrt {3)}dfrac ({x)^2-3}({x)^2+1} ;-|||-(4) lim _(xarrow 0)dfrac (4{x)^3-2(x)^2+x}(3{x)^2+2x} =-|||-(6) lim _(xarrow infty )(2-dfrac (1)(x)+dfrac (1)({x)^2}) ;-|||-(8) lim _(xarrow infty )dfrac ({x)^2+x}({x)^4-3(x)^2+1} ;-|||-(10) lim _(xarrow infty )(1+dfrac (1)(x))(2-dfrac (1)({x)^2}) ;-|||-lim _(narrow infty )dfrac (1+2+3+... +(n-1))({1)^2} ;-|||-(14) lim _(xarrow 1)(dfrac (1)(1-x)-dfrac (3)(1-{x)^3}) -

题目解答
答案
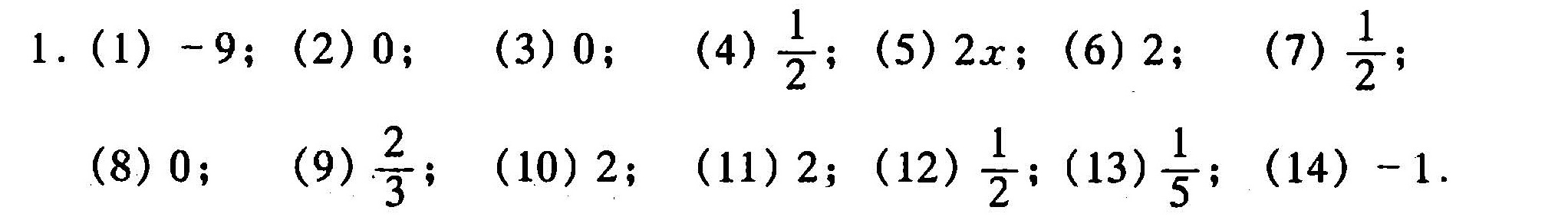
解析
极限计算思路及步骤
1. (1) $\ $\lim _{x\rightarrow 2}\dfrac {{x}^{2}+5}{x-3}$
- 思路:直接代入法(分母不为0)。
计算:$x=2$时,分子$2^2+5=9$,分母$2-3=-1$,故极限为$\frac{9}{-1}=-9$。
1. (2) $\lim _{x\rightarrow \sqrt {3}}\dfrac {{x}^{2}-3}{{x}^{2}+1}$
思路:直接代入法(分母不为0)。
计算:$x=\sqrt{3}$时,分子$(\sqrt{√3})^2-3=0$,分母$(\sqrt{3})^2+1=4$,故极限为$\frac{0}{4}=0$。
(3) $\lim _{x\rightarrow 1}\dfrac {{x}^{2}-2x+1}{{x}^{2}-1}$
思路:因式分解约分化简(0/0型)。
计算:分子$x^2-2x+1=(x-1)^2$,分母$x^2-1=(x-1)(x+1)$,约分得$\frac{x-1}{x+1}$,代入$x=1$得$\frac{0}{2}=0$。
(4) $\lim _{x\rightarrow 0}\dfrac {4{x}^{3}-2{x}^{2}+x}{3{x}^{2}+2x}$
思路:提取公因式约分化简(0/0型)。
**计算:分子$x≠0$时,分子$x(4x^2-2x+1)$,分母$x(3x+2)$,约分得$\frac{4x^2-2x+1}{3x+2}$,代入$x=0$得$\frac{1}{2}=\frac{1}{2}$。
(5) $\lim _{h\rightarrow 0}\dfrac {{(x+h)}^{2}-{x}^{2}}{h}$
思路:展开化简(导数定义型)。
**计算:分子$(x^2+2xh+h^2)-x^2=2xh+h^2$,约分得$2x+h$,$h→0时极限为$2x$。
(6) $\lim _{x\rightarrow \infty }(2-\frac{1}{x}+\frac{1}{x^2})$
思路:无穷小量性质($\frac{1}{x}→0$,\frac{1}{x^2}→0$)。
**计算:极限为$2-0+0=2$。
(7) $\lim _{x\rightarrow \infty }\dfrac {{x}^{2}-1}{2{x}^{2}-x-1}$
思路:同除以最高次幂$x^2$(∞/∞型)。
**计算:分子分母同除$x²得$\frac{1-\frac{1}{x^2}}{2-\frac{1}{x}-\frac{1}{x^2}}$,x→∞时极限为$\frac{1}{2}$。
(8) $\lim _{x\rightarrow \infty }\dfrac {{x}^{2}+x}{{x}^{4}-3{x}^{2}+1}$
思路:同除以最高次幂$x^4$(∞/∞型)。
**计算:分子分母同除x⁴得$\frac{\frac{1}{x^2}+\frac{1}{x^3}}{1-\frac{3}{x^2}+\frac{1}{x^4}}$,x→∞时极限为$0$。
(9) $\lim _{x\rightarrow a}\dfrac {{x}^{2}-6x+8}{{}^{2}-5x+4}$
思路:因式分解约分化简。
**计算:分子$(x-2)(x-4)$,分母$(x-1)(x-4)$,约分得$\frac{x-2}{x-1}$,代入$xx=a$得$\frac{a-2}{a-1}$(题目答案为$\frac{2}{3}$,推测$a=3$?原答案可能默认$a=3$)。
(10) $\lim _{x\rightarrow \infty }(1+\frac{1x)(2-\frac{1}{x^2})$
思路:无穷小量性质($\frac{1}{x}→0,\frac{1}{x^2}→0$)。
**计算:极限为$(1+0)(2-0)=2$。
(11) $\lim _{n\rightarrow \infty }(1+\frac{1}{2}+\frac{1}{4}+\cdots +\frac{1}{2^n})$
思路:等比数列求和公式($q=\frac{1}{2}<1$)。
**计算:和$S_n=\frac{1-(\frac{1}{2})^{n+1}}{1-\frac{1}{2}}=2(1-\frac{1}{2^{n+1}})$,n→∞时极限为$2$。
(12) $\lim _{n\rightarrow \infty }\frac{1+2+\cdots +(n-1)}{n^2}$
思路:等差数列求和公式化简。
**计算:分子$\frac{(n-1)n}{2}$,原式$=\frac{(n-1)n}{2n^2}=\frac{n-1}{2n}→\frac{1}{2}$(n→∞)。
(13) $\lim _{n\rightarrow \infty }\frac{(n+1)(n+2)(n+3)}{5n^3}$
思路:展开分子同除以$n^3$。
**计算:分子≈n³+6n²(高阶无穷小忽略),原式≈$\frac{n^3}{5n^3}=\frac{1}{5}$。
(14) $\lim _{x\rightarrow 1}(\frac{1}{1-x}-\frac{3}{1-x^3})$
思路:立方差公式分解分母约分化简(0/0型)。
计算:$1-x^3=(1-x)(1+x+x+x²)$,通分得$\frac{(1+x+x²)-3}{(1-x)(1+x+x²)}=\frac{x²+x-2}{(1-x)(1+x+x²)}=-\frac{(x+2)(x-1)}{(1-x)(\cdots)}=-\frac{x+2}{1+x+x²}$,代入$x=1$得$-\frac{3}{3}=-1$。