题目
判断函数(x)=ln (sqrt (1+{x)^2}-x)的奇偶性.
判断函数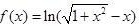 的奇偶性.
的奇偶性.
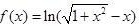 的奇偶性.
的奇偶性.题目解答
答案

解析
考查要点:判断函数的奇偶性,需要掌握奇函数和偶函数的定义,并能通过代数运算验证$f(-x)$与$f(x)$的关系。
解题核心思路:
- 计算$f(-x)$,将原函数中的$x$替换为$-x$,化简表达式。
- 比较$f(-x)$与$f(x)$的关系,若$f(-x) = -f(x)$,则为奇函数;若$f(-x) = f(x)$,则为偶函数。
- 验证定义域是否关于原点对称,确保函数满足奇偶性的判断条件。
破题关键点:
- 对数运算的性质:利用$\ln a + \ln b = \ln(ab)$简化表达式。
- 代数恒等变形:通过乘积展开验证$f(x) + f(-x) = 0$,从而得出$f(-x) = -f(x)$。
步骤1:计算$f(-x)$
将$x$替换为$-x$,得:
$f(-x) = \ln\left(\sqrt{1+(-x)^2} - (-x)\right) = \ln\left(\sqrt{1+x^2} + x\right).$
步骤2:分析$f(x)$与$f(-x)$的关系
计算$f(x) + f(-x)$:
$\begin{aligned}f(x) + f(-x) &= \ln\left(\sqrt{1+x^2} - x\right) + \ln\left(\sqrt{1+x^2} + x\right) \\&= \ln\left[\left(\sqrt{1+x^2} - x\right)\left(\sqrt{1+x^2} + x\right)\right].\end{aligned}$
步骤3:化简乘积
展开括号内的乘积:
$\left(\sqrt{1+x^2} - x\right)\left(\sqrt{1+x^2} + x\right) = (\sqrt{1+x^2})^2 - x^2 = (1+x^2) - x^2 = 1.$
步骤4:得出结论
因此:
$f(x) + f(-x) = \ln(1) = 0 \implies f(-x) = -f(x).$
步骤5:验证定义域
$\sqrt{1+x^2} \geq |x|$,故$\sqrt{1+x^2} - x > 0$对所有$x \in \mathbb{R}$成立,定义域为$\mathbb{R}$,关于原点对称。