题目
解不等式|(x)^2-5x+5|lt 1.
解不等式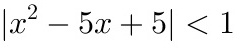 .
.
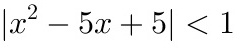 .
.题目解答
答案
解: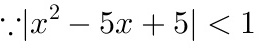 ,
,
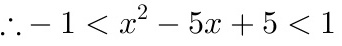 ,
,
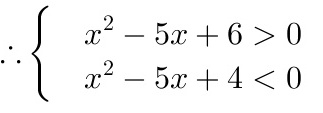 ,即
,即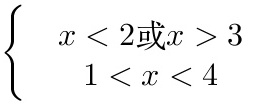 ,
,
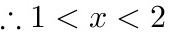 或
或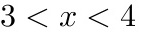 ,
,
 原不等式的解集为:
原不等式的解集为: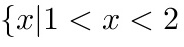 或
或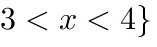 .
.
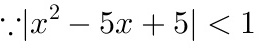 ,
,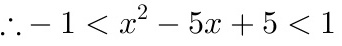 ,
,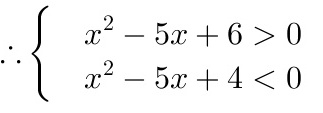 ,即
,即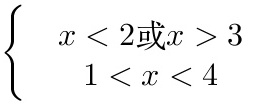 ,
,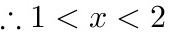 或
或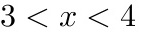 ,
, 原不等式的解集为:
原不等式的解集为: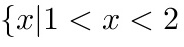 或
或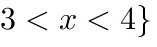 .
.解析
步骤 1:将绝对值不等式转化为两个不等式
由于$|{x}^{2}-5x+5|\lt 1$,根据绝对值的性质,可以转化为两个不等式:${x}^{2}-5x+5\lt 1$和${x}^{2}-5x+5\gt -1$。
步骤 2:解不等式${x}^{2}-5x+5\lt 1$
将不等式${x}^{2}-5x+5\lt 1$转化为${x}^{2}-5x+4\lt 0$,然后求解这个一元二次不等式。
步骤 3:解不等式${x}^{2}-5x+5\gt -1$
将不等式${x}^{2}-5x+5\gt -1$转化为${x}^{2}-5x+6\gt 0$,然后求解这个一元二次不等式。
步骤 4:求解两个不等式的交集
求解步骤2和步骤3中得到的两个不等式的解集的交集,即为原不等式的解集。
由于$|{x}^{2}-5x+5|\lt 1$,根据绝对值的性质,可以转化为两个不等式:${x}^{2}-5x+5\lt 1$和${x}^{2}-5x+5\gt -1$。
步骤 2:解不等式${x}^{2}-5x+5\lt 1$
将不等式${x}^{2}-5x+5\lt 1$转化为${x}^{2}-5x+4\lt 0$,然后求解这个一元二次不等式。
步骤 3:解不等式${x}^{2}-5x+5\gt -1$
将不等式${x}^{2}-5x+5\gt -1$转化为${x}^{2}-5x+6\gt 0$,然后求解这个一元二次不等式。
步骤 4:求解两个不等式的交集
求解步骤2和步骤3中得到的两个不等式的解集的交集,即为原不等式的解集。