题目
【题目】-|||-1 0 1)-|||-设A= 0 2 0 而 geqslant 2 为正整数,则 ^n-2(A)^n-1=-|||-1 0 1

题目解答
答案
最佳答案
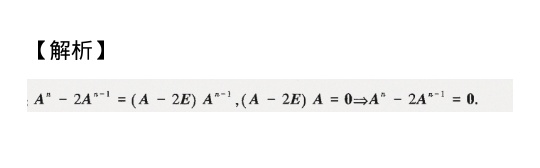
解析
考查要点:本题主要考查矩阵的幂运算性质及矩阵方程的化简技巧,需要学生掌握矩阵乘法的运算规则,并能够灵活运用矩阵的因式分解方法。
解题核心思路:
- 观察矩阵结构:发现矩阵$A$与单位矩阵$E$的线性组合可能具有特殊性质(如零矩阵)。
- 构造关键等式:通过计算$(A - 2E)A$,发现其结果为零矩阵,从而建立递推关系。
- 归纳推广:利用递推关系将高次幂表达式降阶,最终得出结果为零矩阵。
破题关键点:
- 发现$(A - 2E)A = 0$,这是化简高次幂表达式的突破口。
- 因式分解:将$A^n - 2A^{n-1}$分解为$(A - 2E)A^{n-1}$,结合关键等式直接得出结果。
步骤1:验证关键等式
计算$(A - 2E)A$:
$A - 2E = \begin{pmatrix} -1 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & -1 \end{pmatrix}, \quad
(A - 2E)A = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}.$
结论:$(A - 2E)A = 0$。
步骤2:因式分解表达式
将原式分解:
$A^n - 2A^{n-1} = (A - 2E)A^{n-1}.$
步骤3:代入关键等式
由于$(A - 2E)A = 0$,对任意$n \geqslant 2$,有:
$(A - 2E)A^{n-1} = (A - 2E)A \cdot A^{n-2} = 0 \cdot A^{n-2} = 0.$
最终结论:
$A^n - 2A^{n-1} = 0.$