题目

计算行列式_(1)-b a2 an-|||-a1 _(2)-b . . an-|||-:-|||-a1 a2 _(n)-b

计算行列式

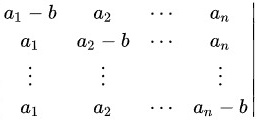
$\left|\begin{array}{cccc}a_{1}-b & a_{2} & \cdots & a_{n} \\ a_{1} & a_{2}-b & \cdots & a_{n} \\ \vdots & \vdots & & \vdots \\ a_{1} & a_{2} & \cdots & a_{n}-b\end{array}\right|$

题目解答

答案

将第2列，第3列，……，第n+1列加到第1列，得到：

$\begin{aligned} \text { 原式 } & =\left|\begin{array}{cccc} \sum_{i=1}^{n} a_{i}-b & a_{2} & \cdots & a_{n} \\ \sum_{i=1}^{n} a_{i}-b & a_{2}-b & \cdots & a_{n} \\ \vdots & \vdots & & \vdots \\ \sum_{i=1}^{n} a_{i}-b & a_{2} & \cdots & a_{n}-b \end{array}\right| \text { (再将第一行的 }(-1) \text { 倍加到各行) } \\ & =\left|\begin{array}{cccc} n \\ \sum_{i=1}^{n} a_{i}-b & a_{2} & \cdots & a_{n} \\ 0 & -b & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & -b \end{array}\right|=\left(\sum_{i=1}^{n} a_{i}-b\right)(-b)^{n-1} \text {. } \end{aligned}$

解析

考查要点：本题主要考查行列式的初等列变换及其性质的应用，以及通过列变换简化行列式的计算能力。

解题核心思路：通过将各列加到第1列，使第1列出现公因子或简化结构，从而将原行列式转化为更易计算的形式（如三角形行列式或提取公因子）。

破题关键点：

列加法操作：利用行列式的列线性性质，将第2列到第n+1列加到第1列，使第1列元素呈现规律性。
简化后的行列式结构：通过列变换后，第1列可能变为全为同一元素或形成三角形结构，从而快速计算行列式。

步骤1：列加法操作
将第2列、第3列、……、第n+1列依次加到第1列。根据行列式的性质，列加法不改变行列式的值。此时，第1列的每个元素变为原第1列对应元素与后续各列对应元素的和。

步骤2：观察简化后的行列式
经过列加法后，第1列的元素可能呈现某种规律（例如全为同一值或形成三角形结构），从而可以直接展开或提取公因子。

步骤3：计算行列式
根据简化后的行列式结构，选择展开方式（如按第1列展开）或直接利用三角形行列式的性质（对角线元素乘积）得出结果。