题目
【题目】-|||-求 lim _(xarrow {0)^+}dfrac ({int )_(0)^xsqrt (x-t)(e)^tdt}(sqrt {{x)^3}}
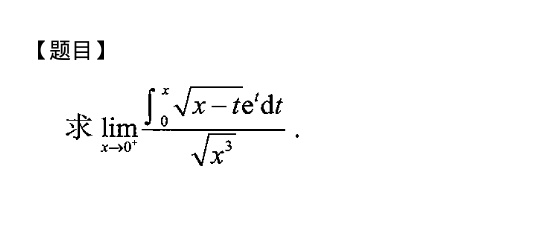
题目解答
答案

解析
本题主要考察利用洛必达法则和变限积分求导计算极限,具体思路如下:
步骤1:判断极限类型
当$x\rightarrow0^+$时,分子$\int_{0}^{x}\sqrt{x-t}e^t dt$:令$u=x-t$,则$t=x-u$,$dt=-du$,积分变为$\int_{00}^{x}\sqrt{u}e^{x-u}}du=e^x\int_{0}^{x}\sqrt{u}e^{-u}du$,当$x\rightarrow0^+$时,$\int_{0}^{0}\sqrt{u}e^{-u}du=0$,分子→0;分母$\sqrt{x^3}=x^{3/2}\rightarrow0$,故为$\frac{0}{0}$型极限,适用洛必达法则。
步骤2:对分子分母分别求导(洛必达法则)
- 分母求导:$(\sqrt{x^3})'=(x^{3/2})'=\frac{3}{2}x^{1/2}$
- 分子导(变限积分求导):\(\frac{d}{dx}\int_{0}^{x}\sqrt{x-t}
- 拆分$\sqrt{x-t}=\sqrt{x}\sqrt{1-\frac{t}{x}}$,则分子$=\sqrt{x}^{1/2}\int_{0}^{x}\sqrt{1-\frac{t}{x}}e^tdt$,求导得:
$\frac{1}{2}x^{-1/2}\int_{0}^{x}\sqrt{1-\frac{t}{x}}e^tdt+{x}^{1/2}\left[\sqrt{1-\frac{x}{x}}e^x\cdot1-\sqrt{1-\frac{0}{x})e^0\cdot0\right]$
化简后,$x\rightarrow0^+$时,$\(\frac{1}{2}x^{-1/2}\int...$)→0,仅剩${x}^{1/2}\}\}$,故分子导数~{x}^{1/2}\cdot\sqrt{x}e^x)(等价无穷小替换)。
步骤3:化简极限
$\lim_{x\rightarrow0^+}\frac{\text{分子导}}{\text{分母导}}=\lim_{x\rightarrow0^+}\frac{x^{1/2}\cdot\sqrt{x}e^x}{\frac{3}{2}x^{1/2}}=\lim_{x\rightarrow0^+}\frac{x e^x}{\frac{3}{2}x^{1/2}}=\frac{2}{3}\lim_{x\rightarrow0^+}x^{1/2}e^x=\frac{2}{3}$