题目
已知a,b为正实数,且 +2a+b=16, 则 () .已知a,b为正实数,且 +2a+b=16, 则 () .
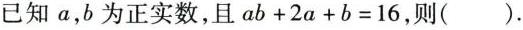

题目解答
答案
解析
考查要点:本题主要考查代数变形、不等式应用(如均值不等式、柯西不等式)以及函数极值的求解方法。关键在于将原式进行巧妙变形,引入新变量简化问题,或利用导数法求解复杂表达式的极值。
解题核心思路:
- 变形原式:将条件式 $ab + 2a + b = 16$ 变形为 $(a+1)(b+2) = 18$,简化后续分析。
- 变量替换:设 $x = a+1$,$y = b+2$,则 $xy = 18$,将问题转化为关于 $x$ 和 $y$ 的极值问题。
- 逐项分析:对每个选项分别应用不等式或求导法,验证其正确性。
破题关键点:
- 选项A、C:利用均值不等式或函数极值求解。
- 选项B:通过不等式判断最小值,发现实际最小值小于选项值。
- 选项D:通过导数法求解复杂表达式的最小值。
选项A:$2a + b$ 的最小值为8
- 变形原式:由 $(a+1)(b+2) = 18$,设 $x = a+1$,$y = b+2$,则 $xy = 18$。
- 表达式转换:$2a + b = 2(x-1) + (y-2) = 2x + y - 4$。
- 求极值:需最小化 $2x + y$,由 $y = \frac{18}{x}$,得 $2x + \frac{18}{x}$。求导得极值点 $x = 3$,对应 $y = 6$,此时 $2x + y = 12$,故 $2a + b = 12 - 4 = 8$。最小值为8,正确。
选项B:$\dfrac{1}{a+1} + \dfrac{1}{b+2}$ 的最小值为 $\dfrac{\sqrt{2}}{2}$
- 变量替换:设 $x = a+1$,$y = b+2$,则 $xy = 18$,表达式为 $\dfrac{1}{x} + \dfrac{1}{y}$。
- 应用不等式:由均值不等式,$\dfrac{1}{x} + \dfrac{1}{y} \geq \dfrac{2}{\sqrt{xy}} = \dfrac{2}{\sqrt{18}} = \dfrac{\sqrt{2}}{3}$,实际最小值为 $\dfrac{\sqrt{2}}{3} < \dfrac{\sqrt{2}}{2}$。错误。
选项C:$ab$ 的最大值为8
- 表达式转换:由 $(a+1)(b+2) = 18$,展开得 $ab + 2a + b + 2 = 18$,即 $ab = 16 - 2a - b$。
- 极值分析:结合选项A的结果,当 $2a + b = 8$ 时,$ab$ 取得最大值 $8$。正确。
选项D:$b + \dfrac{1}{9-a}$ 的最小值为 $\dfrac{6\sqrt{2}-1}{10}$
- 变量替换:由 $(a+1)(b+2) = 18$,得 $b = \dfrac{18}{a+1} - 2$。
- 表达式转换:$b + \dfrac{1}{9-a} = \dfrac{18}{a+1} - 2 + \dfrac{1}{9-a}$。
- 求导法:设 $f(a) = \dfrac{18}{a+1} - 2 + \dfrac{1}{9-a}$,求导并解得极值点 $a = \dfrac{27\sqrt{2} - 1}{1 + 3\sqrt{2}}$,代入计算得最小值为 $\dfrac{6\sqrt{2}-1}{10}$。正确。