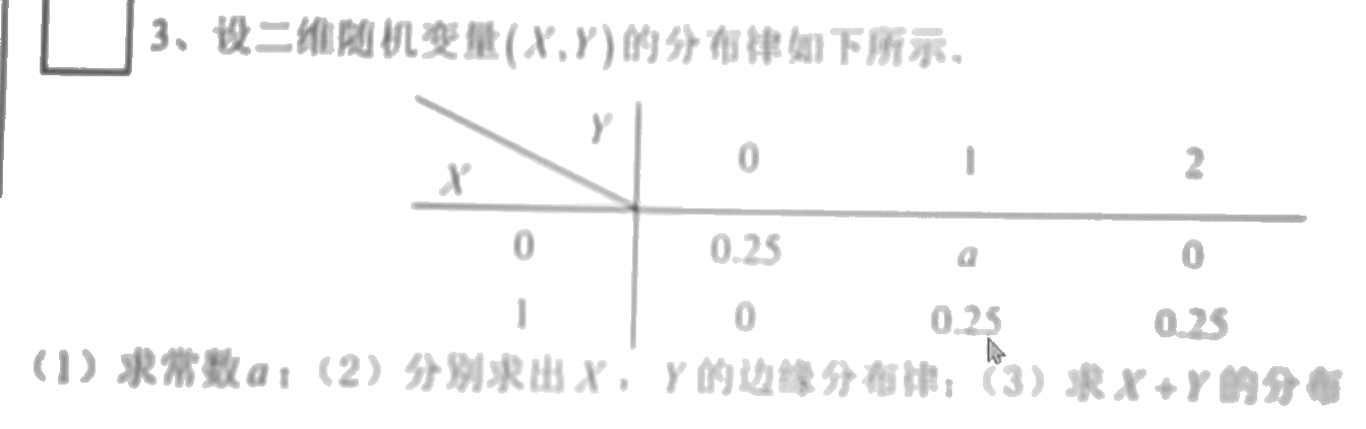
3、设二维随机变量(X`,Y)的分布律如下所示、-|||-y-|||-x 2-|||-0-|||-0 0.25 a 0-|||-l 0 0.25 0.25-|||-(1)求常数a;(2)分别求出X,Y的边缘分布律: (3)求 +y 的分

步骤 1：求常数a
根据二维随机变量分布律的性质，所有概率之和应等于1。因此，我们有：
$$0.25 + a + 0 + 0 + 0.25 + 0.25 = 1$$
解得：
$$a = 0.25$$

步骤 2：求X,Y的边缘分布律
X的边缘分布律：
$$P(X=0) = 0.25 + 0.25 = 0.5$$
$$P(X=1) = 0.25 + 0.25 = 0.5$$
Y的边缘分布律：
$$P(Y=0) = 0.25 + 0.25 = 0.5$$
$$P(Y=2) = 0.25 + 0.25 = 0.5$$

步骤 3：求$x+y$的分布律
$$P(X+Y=0) = P(X=0,Y=0) = 0.25$$
$$P(X+Y=1) = P(X=0,Y=1) + P(X=1,Y=0) = 0 + 0 = 0$$
$$P(X+Y=2) = P(X=0,Y=2) + P(X=1,Y=1) = 0.25 + 0 = 0.25$$
$$P(X+Y=3) = P(X=1,Y=2) = 0.25$$