题目
2.下列函数中相同的是 () .-|||-A. (x)=|x|,g(x)=sqrt ({x)^2} B. (x)=sqrt (1-{cos )^2x} (x)=sin x-|||-℃. (x)=ln (x)^2,g(x)=2ln x D. (x)=dfrac (x)(x),g(x)=1
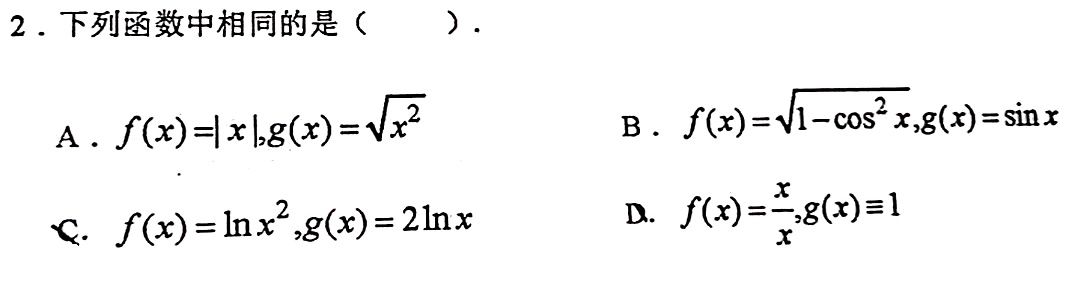
题目解答
答案

解析
步骤 1:分析选项 A
$f(x)=|x|$ 和 $g(x)=\sqrt{{x}^{2}}$,由于 $\sqrt{{x}^{2}}=|x|$,所以这两个函数的定义域和对应法则都相同,因此它们是相同的函数。
步骤 2:分析选项 B
$f(x)=\sqrt{1-{\cos}^{2}x}=\sqrt{{\sin}^{2}x}=|\sin x|$,而 $g(x)=\sin x$,由于 $|\sin x|$ 和 $\sin x$ 的值域不同,所以它们不是相同的函数。
步骤 3:分析选项 C
$f(x)=\ln{x}^{2}$ 的定义域为 $x\neq 0$,而 $g(x)=2\ln x$ 的定义域为 $x>0$,由于定义域不同,所以它们不是相同的函数。
步骤 4:分析选项 D
$f(x)=\dfrac{x}{x}$ 的定义域为 $x\neq 0$,而 $g(x)=1$ 的定义域为 $x\in R$,由于定义域不同,所以它们不是相同的函数。
$f(x)=|x|$ 和 $g(x)=\sqrt{{x}^{2}}$,由于 $\sqrt{{x}^{2}}=|x|$,所以这两个函数的定义域和对应法则都相同,因此它们是相同的函数。
步骤 2:分析选项 B
$f(x)=\sqrt{1-{\cos}^{2}x}=\sqrt{{\sin}^{2}x}=|\sin x|$,而 $g(x)=\sin x$,由于 $|\sin x|$ 和 $\sin x$ 的值域不同,所以它们不是相同的函数。
步骤 3:分析选项 C
$f(x)=\ln{x}^{2}$ 的定义域为 $x\neq 0$,而 $g(x)=2\ln x$ 的定义域为 $x>0$,由于定义域不同,所以它们不是相同的函数。
步骤 4:分析选项 D
$f(x)=\dfrac{x}{x}$ 的定义域为 $x\neq 0$,而 $g(x)=1$ 的定义域为 $x\in R$,由于定义域不同,所以它们不是相同的函数。