题目
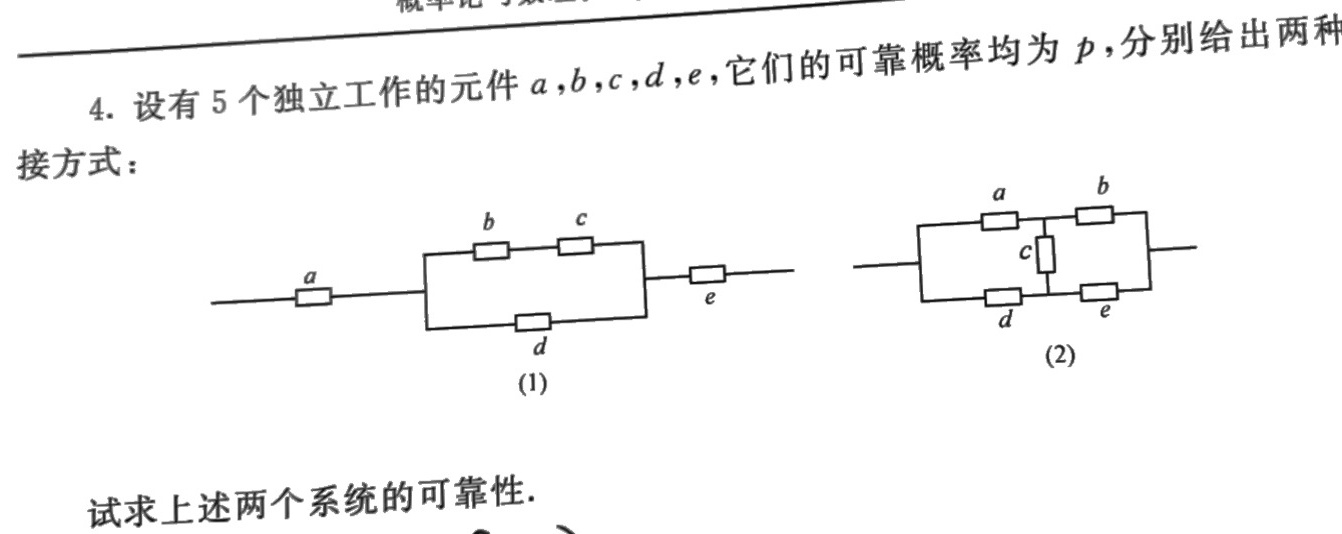
4.设有5个独立作的元件a,b,c,d,e,它们的可靠概率均为p,分别给出两种-|||-接方式:-|||-a b-|||-b c-|||-c-|||-a/□ e-|||-d e-|||-d (2)-|||-(1)-|||-试求上述两个系统的可靠性.
题目解答
答案

解析
考查要点:本题主要考查可靠性概率的计算,涉及独立事件的概率乘法公式和容斥原理的应用。关键在于正确识别电路的并联路径,并准确计算各路径的可靠性及其交集概率。
解题思路:
- 分解路径:将电路分解为若干条独立工作的并联路径。
- 计算单路径概率:每条路径的可靠性为路径中所有元件均正常工作的概率(独立事件乘积)。
- 容斥原理:利用容斥原理计算至少一条路径正常工作的概率,需注意扣除重复计算的交集部分。
破题关键:
- 路径识别:明确不同接法对应的并联路径结构。
- 交集处理:正确计算不同路径同时正常工作的概率,避免遗漏或重复。
(1) 第一种接法:a-b-c-e 和 a-d-e 并联
步骤1:识别并联路径
- 路径1:a → b → c → e(4个元件)
- 路径2:a → d → e(3个元件)
步骤2:计算单路径概率
- 路径1可靠性:$P(\text{abce}) = p^4$
- 路径2可靠性:$P(\text{ade}) = p^3$
步骤3:应用容斥原理
- 至少一条路径正常工作的概率:
$P_0 = P(\text{abce}) + P(\text{ade}) - P(\text{abce}) \cdot P(\text{ade})$ - 交集部分(两路径同时正常)要求所有元件均正常:
$P(\text{abce} \cap \text{ade}) = p^5$
步骤4:代入计算
$P_0 = p^4 + p^3 - p^5$
(2) 第二种接法:复杂并联结构
步骤1:识别并联路径
- 路径1:a → b(2个元件)
- 路径2:a → c → e(3个元件)
- 路径3:d → c → b(3个元件)
- 路径4:d → e(2个元件)
步骤2:计算单路径概率
- 路径1可靠性:$p^2$
- 路径2可靠性:$p^3$
- 路径3可靠性:$p^3$
- 路径4可靠性:$p^2$
步骤3:应用容斥原理
- 总概率需扣除所有路径交集的重复计算:
$P_0 = (p^2 + p^3 + p^3 + p^2) - \text{(两两交集)} + \text{(三三交集)} - \text{(四四交集)}$ - 通过展开计算可得最终表达式:
$P_0 = p^3 - 5p^4 + 2p^5$