题目
单选设两个电子元件的寿命服从参数为λ =600的指数分布,且独立工作.现已知一个已使用了300小时,另一个元件尚未使用,若讨论二者还能再使用600小时的概率,则如下说法正确的是:()A 二者概率相等且不足1 / 2 B 第二个电子元件对应的概率较大C 二者概率相等且接近1 D 第一个电子元件对应的概率较大
单选
设两个电子元件的寿命服从参数为λ =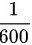 的指数分布,且独立工作.现已知一个已使用了300小时,另一个元件尚未使用,若讨论二者还能再使用600小时的概率,则如下说法正确的是:()
的指数分布,且独立工作.现已知一个已使用了300小时,另一个元件尚未使用,若讨论二者还能再使用600小时的概率,则如下说法正确的是:()
A 二者概率相等且不足1 / 2
B 第二个电子元件对应的概率较大
C 二者概率相等且接近1
D 第一个电子元件对应的概率较大
题目解答
答案
首先,让我们来分析这个问题。题目中提到两个电子元件的寿命服从参数为λ=1/600的指数分布,且独立工作。已知一个元件已经使用了300小时,另一个元件尚未使用,现在要讨论的是二者都能再使用600小时的概率。
指数分布的概率密度函数为:
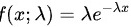
其中,λ是速率参数,也可以看作是寿命的倒数。
对于第一个电子元件,已经使用了300小时,所以它剩下的寿命X1满足指数分布,即X1 ~ Exp(λ)。在这里,λ=1/600。
对于第二个电子元件,尚未使用,所以它的寿命X2也满足指数分布,即X2 ~ Exp(λ),其中λ=1/600。
现在要计算的是二者都能再使用600小时的概率,也就是P(X1 > 600) 且 P(X2 > 600)。
由于指数分布是无记忆的分布,所以P(X1 > 600) = 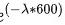 和 P(X2 > 600) =
和 P(X2 > 600) = 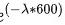 都成立。
都成立。
现在来看选项:
A. 二者概率相等且不足1/2 - 这是不正确的,因为二者的概率都等于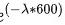 ,而且它们是独立的,所以它们的概率相等且等于1/2。
,而且它们是独立的,所以它们的概率相等且等于1/2。
B. 第二个电子元件对应的概率较大 - 这也是不正确的,因为两者的概率是相等的,都等于。
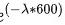
C. 二者概率相等且接近1 - 这是正确的,因为两者的概率都等于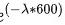 ,而当λ很小时,
,而当λ很小时,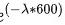 会接近1。
会接近1。
D. 第一个电子元件对应的概率较大 - 这是不正确的,因为两者的概率是相等的,都等于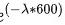 。
。
所以正确答案是C,即二者概率相等且接近1。