题目
任意 阶矩阵 都可以经过初等变换化为单位矩阵 . A. 对 B. 错
任意 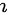 阶矩阵
阶矩阵 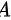 都可以经过初等变换化为单位矩阵 .
都可以经过初等变换化为单位矩阵 .
A. 对
B. 错
题目解答
答案
由逆矩阵的定义:若对于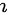 阶矩阵
阶矩阵 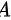 ,如果有一个
,如果有一个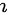 阶矩阵
阶矩阵 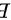 ,使
,使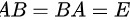 ,则说矩阵
,则说矩阵 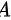 是可逆的,且
是可逆的,且 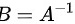
若 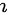 阶矩阵
阶矩阵 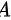 可以经过初等变换化为单位矩阵
可以经过初等变换化为单位矩阵
则 
令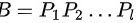
则 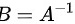 ,即矩阵
,即矩阵 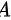 是可逆
是可逆
不是任意矩阵都可逆,故命题”任意 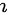 阶矩阵
阶矩阵 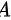 都可以经过初等变换化为单位矩阵”是错误的
都可以经过初等变换化为单位矩阵”是错误的
故本题答案选 B
解析
考查要点:本题主要考查矩阵初等变换与矩阵可逆性的关系,以及学生对逆矩阵存在条件的理解。
解题核心思路:
- 关键点1:只有可逆矩阵(即行列式不为零的矩阵)才能通过初等行变换化为单位矩阵。
- 关键点2:并非所有矩阵都可逆(例如行列式为零的矩阵),因此原命题“任意n阶矩阵都可以经过初等变换化为单位矩阵”是错误的。
破题关键:
通过逆矩阵的定义可知,若矩阵可逆,则存在逆矩阵使得乘积为单位矩阵;而初等变换的本质是左乘初等矩阵,因此若矩阵能化为单位矩阵,则其必可逆。但并非所有矩阵都可逆,故原命题不成立。
逆矩阵的定义:
若n阶矩阵$A$存在n阶矩阵$B$,使得$AB = BA = E$($E$为单位矩阵),则称$A$可逆,$B$为$A$的逆矩阵,记作$B = A^{-1}$。
初等变换与可逆性的关系:
- 若矩阵$A$可通过初等行变换化为单位矩阵$E$,则存在一系列初等矩阵$P_1, P_2, \dots, P_k$,使得:
$A \cdot P_1 P_2 \cdots P_k = E.$
令$B = P_1 P_2 \cdots P_k$,则$AB = E$,即$B = A^{-1}$,说明$A$可逆。 - 反之,若$A$可逆,则必存在有限次初等变换将其化为$E$。
结论:
由于并非所有n阶矩阵都可逆(例如行列式为零的矩阵),因此原命题“任意n阶矩阵都可以经过初等变换化为单位矩阵”是错误的。