题目
下列函数中，是偶函数的是( )A.(x)=(x)^2sin xB.(x)=(x)^2sin xC.(x)=(x)^2sin xD.(x)=(x)^2sin x
下列函数中，是偶函数的是( )
A.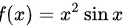
B.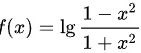
C.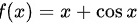
D.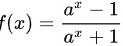
题目解答
答案
根据偶函数的定义：
选项A：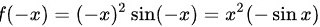
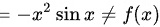，不是偶函数.
选项B：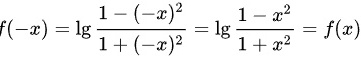
，是偶函数.
选项C：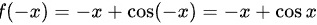
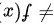，不是偶函数.
选项D：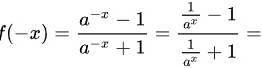
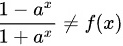，不是偶函数.
综上，答案是选项B
解析
步骤 1：定义偶函数
偶函数的定义是：对于函数$f(x)$，如果对于所有$x$，都有$f(-x) = f(x)$，则$f(x)$是偶函数。
步骤 2：分析选项A
$f(x) = x^2\sin x$，则$f(-x) = (-x)^2\sin(-x) = x^2(-\sin x) = -x^2\sin x$，所以$f(-x) \neq f(x)$，不是偶函数。
步骤 3：分析选项B
$f(x) = \lg \dfrac{1-x^2}{1+x^2}$，则$f(-x) = \lg \dfrac{1-(-x)^2}{1+(-x)^2} = \lg \dfrac{1-x^2}{1+x^2} = f(x)$，所以$f(-x) = f(x)$，是偶函数。
步骤 4：分析选项C
$f(x) = x + \cos x$，则$f(-x) = -x + \cos(-x) = -x + \cos x$，所以$f(-x) \neq f(x)$，不是偶函数。
步骤 5：分析选项D
$f(x) = \dfrac{a^x - 1}{a^x + 1}$，则$f(-x) = \dfrac{a^{-x} - 1}{a^{-x} + 1} = \dfrac{\frac{1}{a^x} - 1}{\frac{1}{a^x} + 1} = \dfrac{1 - a^x}{1 + a^x}$，所以$f(-x) \neq f(x)$，不是偶函数。
偶函数的定义是：对于函数$f(x)$，如果对于所有$x$，都有$f(-x) = f(x)$，则$f(x)$是偶函数。
步骤 2：分析选项A
$f(x) = x^2\sin x$，则$f(-x) = (-x)^2\sin(-x) = x^2(-\sin x) = -x^2\sin x$，所以$f(-x) \neq f(x)$，不是偶函数。
步骤 3：分析选项B
$f(x) = \lg \dfrac{1-x^2}{1+x^2}$，则$f(-x) = \lg \dfrac{1-(-x)^2}{1+(-x)^2} = \lg \dfrac{1-x^2}{1+x^2} = f(x)$，所以$f(-x) = f(x)$，是偶函数。
步骤 4：分析选项C
$f(x) = x + \cos x$，则$f(-x) = -x + \cos(-x) = -x + \cos x$，所以$f(-x) \neq f(x)$，不是偶函数。
步骤 5：分析选项D
$f(x) = \dfrac{a^x - 1}{a^x + 1}$，则$f(-x) = \dfrac{a^{-x} - 1}{a^{-x} + 1} = \dfrac{\frac{1}{a^x} - 1}{\frac{1}{a^x} + 1} = \dfrac{1 - a^x}{1 + a^x}$，所以$f(-x) \neq f(x)$，不是偶函数。