向量的概念①向量 既有大小又有方向的量。向量的大小即向量的模(长度),记作|AB|AB即向量的大小,记作|AB|。]向量不能比较大小,但向量的模可以比较大小。向量表示方法:(1)几何表示法:用带箭头的有向线段表示,如AB,注意起点在前,终点在后;(2)符号表示法:用一个小写的英文字母来表示,如AB,AB,AB等;(3)坐标表示法:在平面内建立直角坐标系,以与AB轴、AB轴方向相同的两个单位向量AB,AB为基底,则平面内的任一向量AB可表示为AB,称AB为向量AB的坐标,AB=AB叫做向量AB的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。向量和数量的区别:向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。如已知A(1,2),B(4,2),则把向量AB按向量AB=(-1,3)平移后得到的向量是_____(答:(3,0))②零向量[ 长度为0的向量,记为AB,其方向是任意的,AB与任意向量平行AB零向量AB=ABAB|AB|=0。由于AB的方向是任意的,AB且规定AB平行于任何向量,故在有AB关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件。(注意与0的区别)③单位向量 模为1个单位长度的向量,向量AB为单位向量AB|AB|=1。(与AB共线的单位向量是AB);④平行向量(共线向量)方向相同或相反的非零向量ABAB。任意一组AB平行向量都可以移到同一直线上,方向相同或相反的向量,称为平行向量,记作AB∥AB,规定零向量和任何向量平行。由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量。提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有AB);④三点AB共线ABAB共线;由题意得AB,得AB或AB。例7.已知AB(1)求AB;(2)当AB为何实数时,ABABAB与AB平行, 平行时它们是同向还是反向?解析:(1)因为AB所以AB则AB(2)ABABABAB,ABAB因为ABABAB与AB平行,所以AB即得AB。此AB时ABABABAB,ABAB,则ABAB,即此时向量AB与AB方向相反。点评:上面两个例子重点解析了平面向量的性质在坐标运算中的体现,重点掌握平面向量的共线的判定以及平面向量模的计算方法。题型5:共线向量定理及平面向量基本定理例8.平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足AB,其中α、β∈R,且α+β=1,则点C的轨迹方程为( )A. 3x+2y-11=0 B. (x-1)2+(y-2)2=5 C. 2x-y=0 D. x+2y-5=0 E. 解法一:设AB,则AB。 F. [来源:学+科+网Z+X+X+K] G. 于是AB,先消去AB,由AB得AB。 。 解法二:由平面向量共线定理, C共线。 的轨迹为直线AB,由两点式直线方程得AB即选 。 点评:熟练运用向量的加法、减法、实数与向量的积的坐标运算法则进行运算;两个向量平行的坐标表示;运用向量的坐标表示,使向量的运算完全代数化,将数与形有机的结合。 题型6:数量积的概念 例9.判断下列各命题正确与否: (1)AB; (2)AB; (3)若AB,则AB; (4)若AB,则AB当且仅当AB时成立; (5)AB对任意AB向量都成立; (6)对任意向量AB,有AB。 [来源:学|科|网Z|X|X|K] 点评:通过该题我们清楚了向量的数乘与数量积之间的区别于联系,重点清楚AB为零向量,而AB为零。 R,则下列等式不一定成立的是( ) ABAB AB m(AB)=mAB+mAB AB [来源:学,科,网Z,X,X,K] [来源:学*科*网Z*X*X*K] ①② ②③ ③④ D.②④ ;因为AB,而AB;而AB方向与AB方向不一定同向。 ①平面向量的数量积不满足结合律。故①假;②由向量的减法运算可知|AB|、|AB|、|AB-AB|恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因AB为[(AB·AB)AB-(AB·AB)AB]·AB=(AB·AB)AB·AB-(AB·AB)AB·AB=0,所以垂直.故③假;④(3AB+2AB)(3AB-2AB)=9·AB·AB-4AB·AB=9|AB|2-4|AB|2成立。故④真。 点评:本题考查平面向量的数量积及运算律,向量的数量积运算不满足结合律。 题型7:向量的夹角 例11. (1)已知向量AB、AB满足AB、AB,且AB,则AB与AB的夹角为( ) AB AB AB AB (2)已知向量AB=(cosAB,sinAB),AB=(cosAB,sinAB),且ABABAB,那么AB与AB的夹角的大小是 (3)已知两单位向量AB与AB的夹角为AB,若AB,试求AB与AB的夹角。 (4)| AB|=1,|AB AB |=2,AB= AB+ AB,且AB⊥AB,则向量AB与AB的夹角为AB ( ) 30° 60° C.120° D.150° ;(2)AB; (3)由题意,AB,且AB与ABAB的夹角为AB,所以,AB, ABABAB,AB,同理可得AB。 而ABAB, 设AB为AB与AB的AB夹角,则AB。 ;设所求两向量的夹角为AB ABAB AB 即:AB 所以AB 点评AB:解决向量的夹角问题时要借助于公式AB,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于AB这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握。 例12.(1)设平面向量AB、AB、AB的和AB。如果向量AB、AB、AB,满足AB,且AB顺AB时针旋转AB后与AB同AB向,其中AB,则( ) -AB+AB+AB=AB AB-AB+AB=AB AB+AB-AB=ABAB AB+AB+AB=AB (2)已知AB 且关于AB的方程AB有实根, 则AB与AB的夹角的取值范围是( ) AB AB AB D.AB ;AB(2)B; 点评:对于平面向量的数量积要AB学会技巧性应用,解决好实际问题。 题型8:向量的模 例13.(1)AB已知向量AB与AB的夹角为AB,AB则AB等于( ) 5 4 3 1 (2)设向量AB满足AB,AB,则AB( ) 1 B.2AB C.4 D.5 ;(2)D; 点评:掌握向量数量积的逆运算AB,以及AB。 题型9AB:向量垂直、AB平行的判定 例14.已知向量AB,AB,且AB,则AB 。 解析:∵AB,AB∴AB,∴AB,∴AB。 例15.已知AB,AB,ABAB,按下列条件求实数AB的值。 (1)AB;(2)AB;AB。 [来源:学,科,网] (1)ABABAB; (2)ABABAB; ABAB AB。 点评:此例展示了向量在坐标形式下的平行、垂直、模的基本运算。
向量的概念
①向量 既有大小又有方向的量。向量的大小即向量的模(长度),记作|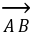 |
| 即向量的大小,记作|
即向量的大小,记作|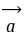 |。]向量不能比较大小,但向量的模可以比较大小。
|。]向量不能比较大小,但向量的模可以比较大小。
向量表示方法:(1)几何表示法:用带箭头的有向线段表示,如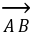 ,注意起点在前,终点在后;(2)符号表示法:用一个小写的英文字母来表示,如
,注意起点在前,终点在后;(2)符号表示法:用一个小写的英文字母来表示,如 ,
, ,
,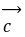 等;(3)坐标表示法:在平面内建立直角坐标系,以与
等;(3)坐标表示法:在平面内建立直角坐标系,以与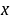 轴、
轴、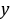 轴方向相同的两个单位向量
轴方向相同的两个单位向量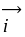 ,
,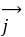 为基底,则平面内的任一向量
为基底,则平面内的任一向量 可表示为
可表示为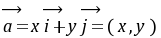 ,称
,称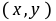 为向量
为向量 的坐标,
的坐标, =
=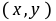 叫做向量
叫做向量 的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
的坐标表示。如果向量的起点在原点,那么向量的坐标与向量的终点坐标相同。
向量和数量的区别:向量常用有向线段来表示,注意不能说向量就是有向线段,为什么?(向量可以平移)。如已知A(1,2),B(4,2),则把向量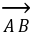 按向量
按向量 =(-1,3)平移后得到的向量是_____(答:(3,0))
=(-1,3)平移后得到的向量是_____(答:(3,0))
②零向量[ 长度为0的向量,记为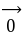 ,其方向是任意的,
,其方向是任意的,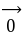 与任意向量平行
与任意向量平行 零向量
零向量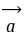 =
=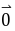
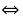 |
|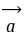 |=0。由于
|=0。由于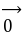 的方向是任意的,
的方向是任意的, 且规定
且规定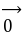 平行于任何向量,故在有
平行于任何向量,故在有 关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件。(注意与0的区别)
关向量平行(共线)的问题中务必看清楚是否有“非零向量”这个条件。(注意与0的区别)
③单位向量 模为1个单位长度的向量,向量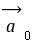 为单位向量
为单位向量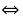 |
|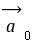 |=1。(与
|=1。(与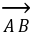 共线的单位向量是
共线的单位向量是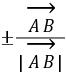 );
);
④平行向量(共线向量)
方向相同或相反的非零向量
 。任意一组
。任意一组 平行向量都可以移到同一直线上,方向相同或相反的向量,称为平行向量,记作
平行向量都可以移到同一直线上,方向相同或相反的向量,称为平行向量,记作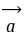 ∥
∥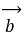 ,规定零向量和任何向量平行。由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量。
,规定零向量和任何向量平行。由于向量可以进行任意的平移(即自由向量),平行向量总可以平移到同一直线上,故平行向量也称为共线向量。
提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有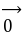 );④三点
);④三点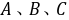 共线
共线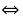
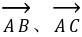 共线;
共线;
由题意得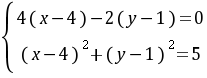 ,得
,得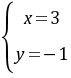 或
或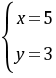 。
。
例7.已知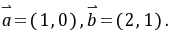 (1)求
(1)求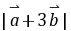 ;(2)当
;(2)当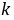 为何实数时,
为何实数时,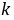
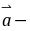
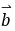 与
与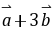 平行, 平行时它们是同向还是反向?
平行, 平行时它们是同向还是反向?
解析:(1)因为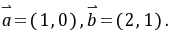 所以
所以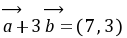 则
则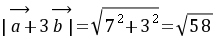
(2)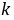
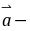
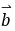
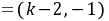 ,
,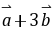
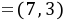 因为
因为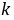
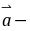
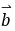 与
与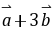 平行,所以
平行,所以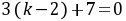 即得
即得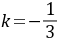 。此
。此 时
时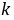
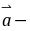
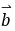
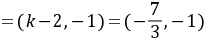 ,
,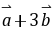
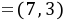 ,则
,则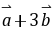
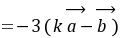 ,即此时向量
,即此时向量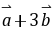 与
与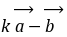 方向相反。
方向相反。
点评:上面两个例子重点解析了平面向量的性质在坐标运算中的体现,重点掌握平面向量的共线的判定以及平面向量模的计算方法。
题型5:共线向量定理及平面向量基本定理
例8.平面直角坐标系中,O为坐标原点,已知两点A(3,1),B(-1,3),若点C满足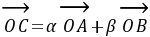 ,其中α、β∈R,且α+β=1,则点C的轨迹方程为( )
,其中α、β∈R,且α+β=1,则点C的轨迹方程为( )
B. (x-1)2+(y-2)2=5
C. 2x-y=0
D. x+2y-5=0
E. 解法一:设
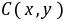 ,则
,则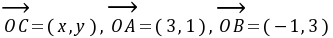 。
。F. [来源:学+科+网Z+X+X+K]
G. 于是
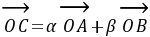 ,先消去
,先消去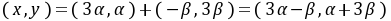 ,由
,由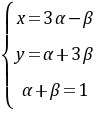 得
得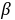 。
。。
解法二:由平面向量共线定理,
C共线。
的轨迹为直线AB,由两点式直线方程得
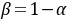 即选
即选。
点评:熟练运用向量的加法、减法、实数与向量的积的坐标运算法则进行运算;两个向量平行的坐标表示;运用向量的坐标表示,使向量的运算完全代数化,将数与形有机的结合。
题型6:数量积的概念
例9.判断下列各命题正确与否:
(1)
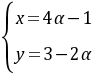 ; (2)
; (2)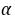 ; (3)若
; (3)若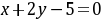 ,则
,则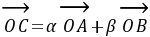 ;
;(4)若
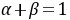 ,则
,则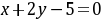 当且仅当
当且仅当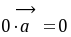 时成立;
时成立;(5)
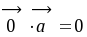 对任意
对任意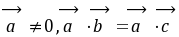 向量都成立; (6)对任意向量
向量都成立; (6)对任意向量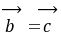 ,有
,有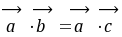 。
。[来源:学|科|网Z|X|X|K]
点评:通过该题我们清楚了向量的数乘与数量积之间的区别于联系,重点清楚
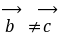 为零向量,而
为零向量,而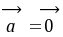 为零。
为零。R,则下列等式不一定成立的是( )
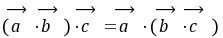
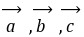
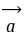
m(
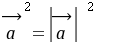 )=m
)=m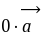 +m
+m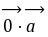

[来源:学,科,网Z,X,X,K]
[来源:学*科*网Z*X*X*K]
①②
②③
③④ D.②④
;因为
 ,而
,而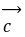 ;而
;而 方向与
方向与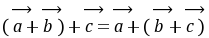 方向不一定同向。
方向不一定同向。①平面向量的数量积不满足结合律。故①假;②由向量的减法运算可知|
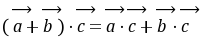 |、|
|、|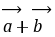 |、|
|、| -
- |恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因
|恰为一个三角形的三条边长,由“两边之差小于第三边”,故②真;③因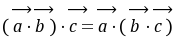 为[(
为[( ·
· )
) -(
-(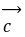 ·
· )
) ]·
]·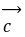 =(
=(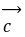 ·
· )
) ·
·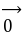 -(
-( ·
· )
) ·
· =0,所以垂直.故③假;④(3
=0,所以垂直.故③假;④(3 +2
+2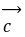 )(3
)(3 -2
-2 )=9·
)=9·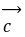 ·
· -4
-4 ·
·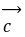 =9|
=9| |2-4|
|2-4| |2成立。故④真。
|2成立。故④真。点评:本题考查平面向量的数量积及运算律,向量的数量积运算不满足结合律。
题型7:向量的夹角
例11.
(1)已知向量
 、
、 满足
满足 、
、 ,且
,且 ,则
,则 与
与 的夹角为( )
的夹角为( )



(2)已知向量
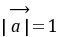 =(cos
=(cos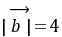 ,sin
,sin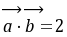 ),
), =(cos
=(cos ,sin
,sin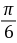 ),且
),且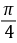
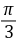
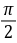 ,那么
,那么 与
与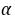 的夹角的大小是
的夹角的大小是(3)已知两单位向量
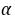 与
与 的夹角为
的夹角为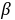 ,若
,若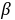 ,试求
,试求 与
与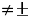 的夹角。
的夹角。(4)|
 |=1,|
|=1,|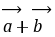
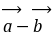 |=2,
|=2,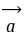 =
= 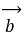 +
+ 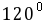 ,且
,且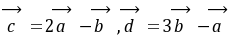 ⊥
⊥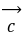 ,则向量
,则向量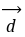 与
与 的夹角为
的夹角为 ( )
( )30°
60° C.120° D.150°
;(2)
 ;
;(3)由题意,
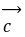 ,且
,且 与
与
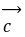 的夹角为
的夹角为 ,所以,
,所以, ,
,
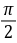 ,
,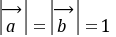 ,同理可得
,同理可得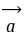 。
。而
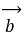 ,
,设
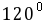 为
为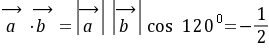 与
与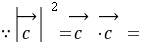 的
的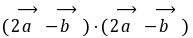 夹角,则
夹角,则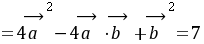 。
。;设所求两向量的夹角为
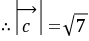
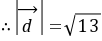
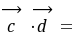
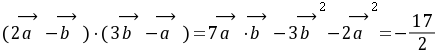 即:
即: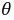 所以
所以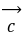
点评
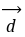 :解决向量的夹角问题时要借助于公式
:解决向量的夹角问题时要借助于公式 ,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于
,要掌握向量坐标形式的运算。向量的模的求法和向量间的乘法计算可见一斑。对于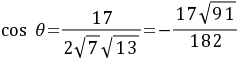 这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握。
这个公式的变形应用应该做到熟练,另外向量垂直(平行)的充要条件必需掌握。例12.(1)设平面向量
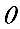 、
、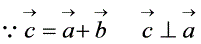 、
、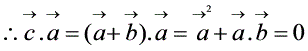 的和
的和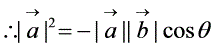 。如果向量
。如果向量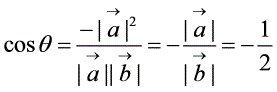 、
、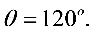 、
、 ,满足
,满足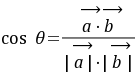 ,且
,且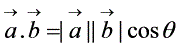 顺
顺 时针旋转
时针旋转 后与
后与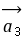 同
同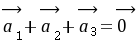 向,其中
向,其中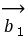 ,则( )
,则( )-
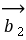 +
+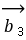 +
+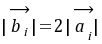 =
=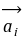
 -
-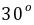 +
+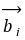 =
=
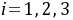 +
+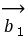 -
-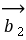 =
=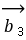
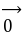
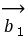 +
+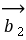 +
+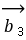 =
=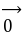
(2)已知
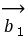 且关于
且关于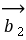 的方程
的方程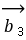 有实根, 则
有实根, 则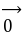 与
与 的夹角的取值范围是( )
的夹角的取值范围是( )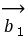
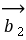
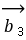 D.
D.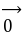
;
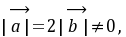 (2)B;
(2)B;点评:对于平面向量的数量积要
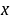 学会技巧性应用,解决好实际问题。
学会技巧性应用,解决好实际问题。题型8:向量的模
例13.(1)
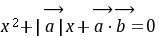 已知向量
已知向量 与
与 的夹角为
的夹角为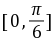 ,
, 则
则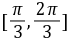 等于( )
等于( )5
4
3
1
(2)设向量
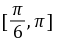 满足
满足 ,
, ,则
,则 ( )
( )1 B.2
 C.4 D.5
C.4 D.5;(2)D;
点评:掌握向量数量积的逆运算
 ,以及
,以及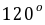 。
。题型9
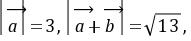 :向量垂直、
:向量垂直、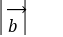 平行的判定
平行的判定例14.已知向量
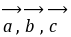 ,
,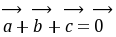 ,且
,且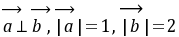 ,则
,则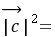 。
。解析:∵
 ,
,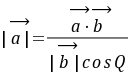 ∴
∴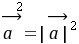 ,∴
,∴ ,∴
,∴ 。
。例15.已知
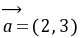 ,
,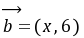 ,
,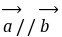
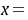 ,按下列条件求实数
,按下列条件求实数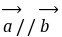 的值。
的值。(1)
 ;(2)
;(2)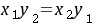 ;
;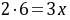 。
。[来源:学,科,网]
(1)
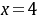
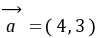
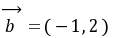 ;
;(2)
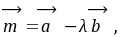
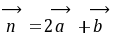
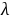 ;
;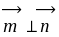
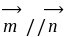
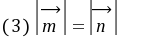 。
。点评:此例展示了向量在坐标形式下的平行、垂直、模的基本运算。
题目解答
答案
[来源:学+科+网Z+X+X+K] [来源:学|科|网Z|X|X|K] [来源:学,科,网Z,X,X,K] [来源:学*科*网Z*X*X*K] [来源:学,科,网]