题目
计算下列极限lim _(xarrow 0)(x)^2sin dfrac (1)(x)lim _(xarrow 0)(x)^2sin dfrac (1)(x)
计算下列极限
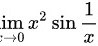
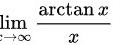
题目解答
答案
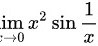
当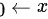 时,
时,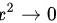 ,是无穷小量,
,是无穷小量,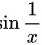 是有界函数,由无穷小
是有界函数,由无穷小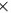 有界函数
有界函数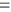 无穷小,得到:
无穷小,得到:
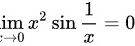
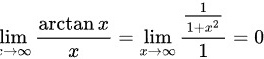
综上,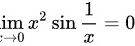 ,
,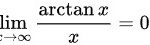
解析
考查要点
- 无穷小量与有界函数的乘积性质:当一个函数是无穷小量,另一个是有界函数时,它们的乘积仍是无穷小量。
- 极限的求解方法:包括直接代入法、洛必达法则、夹逼定理等。
解题核心思路
- 第一题:利用 $x^2$ 在 $x \to 0$ 时为无穷小量,而 $\sin \frac{1}{x}$ 的绝对值不超过 1(有界),直接应用无穷小量与有界函数的乘积性质。
- 第二题:当 $x \to \infty$ 时,$\arctan x$ 趋近于 $\frac{\pi}{2}$,而分母 $x$ 趋近于无穷大,可通过 比较分子分母的增长速度 或 洛必达法则 求解。
第一题:$\lim _{x\rightarrow 0}{x}^{2}\sin \dfrac {1}{x}$
分析函数性质
- $x^2$ 的行为:当 $x \to 0$ 时,$x^2 \to 0$,即 $x^2$ 是无穷小量。
- $\sin \frac{1}{x}$ 的行为:虽然 $\sin \frac{1}{x}$ 在 $x \to 0$ 时振荡,但其绝对值恒满足 $|\sin \frac{1}{x}| \leq 1$,即为有界函数。
应用乘积性质
根据 无穷小量与有界函数的乘积仍为无穷小量,可得:
$\lim _{x\rightarrow 0}{x}^{2}\sin \dfrac {1}{x} = 0.$
第二题:$\lim _{x\rightarrow \infty }\dfrac {\arctan x}{x}$
方法一:直接比较增长速度
- 分子:当 $x \to \infty$ 时,$\arctan x \to \dfrac{\pi}{2}$(趋近于常数)。
- 分母:$x \to \infty$(线性增长)。
因此,分子增长速度远慢于分母,整体极限为 $0$。
方法二:洛必达法则
原式为 $\dfrac{\infty}{\infty}$ 型不定式,可对分子分母分别求导:
$\lim _{x\rightarrow \infty }\dfrac {\dfrac{d}{dx}(\arctan x)}{\dfrac{d}{dx}(x)} = \lim _{x\rightarrow \infty }\dfrac{\dfrac{1}{1+x^2}}{1} = 0.$