题目
设每分钟通过某交叉路口的汽车流量X服从参数为1的泊松分布,则在一分钟内至少有一辆车通过的概率为________.
设每分钟通过某交叉路口的汽车流量X服从参数为1的泊松分布,则在一分钟内至少有一辆车通过的概率为________.
题目解答
答案
根据泊松分布的概率公式：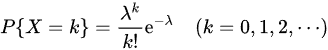
，根据题意，λ=1.因此可以得到
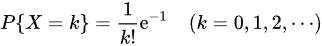，因此可以得到P{X=0}=
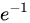.因此可以得到在一分钟内至少有一辆车通过的概率为P{X≥1}=1-P{X=0}=
.
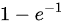解析
步骤 1：泊松分布的概率公式
泊松分布的概率公式为：$P\{ X=k\} =\dfrac {{X}^{k}}{k!}{e}^{-\lambda }$，其中$\lambda$是泊松分布的参数，$k$是事件发生的次数。
步骤 2：确定参数$\lambda$
根据题意，每分钟通过某交叉路口的汽车流量X服从参数为1的泊松分布，因此$\lambda=1$。
步骤 3：计算在一分钟内至少有一辆车通过的概率
在一分钟内至少有一辆车通过的概率为$P\{ X\geq 1\}$，可以表示为$1-P\{ X=0\}$。根据泊松分布的概率公式，$P\{ X=0\} =\dfrac {1^{0}}{0!}{e}^{-1}={e}^{-1}$。因此，$P\{ X\geq 1\} =1-P\{ X=0\} =1-{e}^{-1}$。
泊松分布的概率公式为：$P\{ X=k\} =\dfrac {{X}^{k}}{k!}{e}^{-\lambda }$，其中$\lambda$是泊松分布的参数，$k$是事件发生的次数。
步骤 2：确定参数$\lambda$
根据题意，每分钟通过某交叉路口的汽车流量X服从参数为1的泊松分布，因此$\lambda=1$。
步骤 3：计算在一分钟内至少有一辆车通过的概率
在一分钟内至少有一辆车通过的概率为$P\{ X\geq 1\}$，可以表示为$1-P\{ X=0\}$。根据泊松分布的概率公式，$P\{ X=0\} =\dfrac {1^{0}}{0!}{e}^{-1}={e}^{-1}$。因此，$P\{ X\geq 1\} =1-P\{ X=0\} =1-{e}^{-1}$。