题目
设X为随机变量,其方差存在,c为任意非零常数,则下列等式中正确的是( )A. (x+c)=D(x). B. (x+c)=D(x)+c.-|||-C. D(x-c)=D(x)-c D. (Cx)=cD(x)-|||-得 评卷-|||-分 人 二、填空题(每空 3分,共 15-|||-6.设3阶矩阵A的特征值为 --1, 1,2,它的伴随矩阵记为A×,则-|||-|A*3|-2E|= __ 。-|||-0 -1 (-2 0 0-|||-7.设A= -1 0 1 0 x 0 则 x= __ 。-|||-1 1 0 0 0 1-|||-8.设有3个元件并联,已知每个元件正常工作的概率为P,则该系统-|||-正常工作的概率为 __ 。。-|||-9.设随机变量X的概率密度函数为 f(x)= )= __-|||-10.设二维连续型随机变量(X,Y)的联合概率密度函数为-|||-(x,y)= {e)^-(3x+4y)与xgt 0,ygt 0 则系数 k= __ 。A. (x+c)=D(x). B. (x+c)=D(x)+c.-|||-C. D(x-c)=D(x)-c D. (Cx)=cD(x)-|||-得 评卷-|||-分 人 二、填空题(每空 3分,共 15-|||-6.设3阶矩阵A的特征值为 --1, 1,2,它的伴随矩阵记为A×,则-|||-|A*3|-2E|= __ 。-|||-0 -1 (-2 0 0-|||-7.设A= -1 0 1 0 x 0 则 x= __ 。-|||-1 1 0 0 0 1-|||-8.设有3个元件并联,已知每个元件正常工作的概率为P,则该系统-|||-正常工作的概率为 __ 。。-|||-9.设随机变量X的概率密度函数为 f(x)= )= __-|||-10.设二维连续型随机变量(X,Y)的联合概率密度函数为-|||-(x,y)= {e)^-(3x+4y)与xgt 0,ygt 0 则系数 k= __ 。13.设二维随机变量的联合概率函数是A. (x+c)=D(x). B. (x+c)=D(x)+c.-|||-C. D(x-c)=D(x)-c D. (Cx)=cD(x)-|||-得 评卷-|||-分 人 二、填空题(每空 3分,共 15-|||-6.设3阶矩阵A的特征值为 --1, 1,2,它的伴随矩阵记为A×,则-|||-|A*3|-2E|= __ 。-|||-0 -1 (-2 0 0-|||-7.设A= -1 0 1 0 x 0 则 x= __ 。-|||-1 1 0 0 0 1-|||-8.设有3个元件并联,已知每个元件正常工作的概率为P,则该系统-|||-正常工作的概率为 __ 。。-|||-9.设随机变量X的概率密度函数为 f(x)= )= __-|||-10.设二维连续型随机变量(X,Y)的联合概率密度函数为-|||-(x,y)= {e)^-(3x+4y)与xgt 0,ygt 0 则系数 k= __ 。求:(1)常数c;(2)概率P(X≥Y );(3)X与Y相互独立吗?请说出理由。14.将n个球随机的放入N个盒子中去,设每个球放入各个盒子是等可能的,求有球盒子数X的数学期望。15.设一口袋中依此标有1,2,2,2,3,3数字的六个球。从中任取一球,记随机变量X为取得的球上标有的数字,求(1)X的概率分布律和分布函数。(2)EX得分四、证明题(共10分)评卷人16.设a=(a1,a2,…,an)T,a1≠0,其长度为║a║,又A=aaT,(1)证明A2=║a║2A;(2)证明a是A的一个特征向量,而0是A的n-1重特征值;(3)A能相似于对角阵Λ吗?若能,写出对角阵Λ.得分五、应用题(共10分)评卷人17.设在国际市场上每年对我国某种出口商品的需求量X是随机变量,它在[2000,4000]( 单位:吨 )上服从均匀分布,又设每售出这种商品一吨,可为国家挣得外汇3万元,但假如销售不出而囤积在仓库,则每吨需保养费1万元。问需要组织多少货源,才能使国家收益最大。
设X为随机变量,其方差存在,c为任意非零常数,则下列等式中正确的是( )


13.设二维随机变量的联合概率函数是
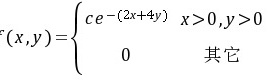
求:(1)常数c;(2)概率P(X≥Y );(3)X与Y相互独立吗?请说出理由。
14.将n个球随机的放入N个盒子中去,设每个球放入各个盒子是等可能的,求有球盒子数X的数学期望。
15.设一口袋中依此标有1,2,2,2,3,3数字的六个球。从中任取一球,记随机变量X为取得的球上标有的数字,求
(1)X的概率分布律和分布函数。(2)EX
得分
四、证明题(共10分)
评卷人
16.设a=(a1,a2,…,an)T,a1≠0,其长度为║a║,又A=aaT,
(1)证明A2=║a║2A;
(2)证明a是A的一个特征向量,而0是A的n-1重特征值;
(3)A能相似于对角阵Λ吗?若能,写出对角阵Λ.
得分
五、应用题(共10分)
评卷人
17.设在国际市场上每年对我国某种出口商品的需求量X是随机变量,它在[2000,4000]( 单位:吨 )上服从均匀分布,又设每售出这种商品一吨,可为国家挣得外汇3万元,但假如销售不出而囤积在仓库,则每吨需保养费1万元。问需要组织多少货源,才能使国家收益最大。
题目解答
答案
A
解析
本题考查方差的基本性质,特别是常数项对方差的影响。解题的关键在于理解:
- 方差反映的是随机变量的离散程度,与常数项无关;
- 常数项的方差为0,且加减常数不会改变方差;
- 乘以常数时方差会乘以该常数的平方。
选项分析
选项A:$D(X+C)=D(X)$
- 正确。根据方差性质,加减常数项不改变方差,即$D(X+C)=D(X)$。
选项B:$D(X+C)=D(X)+C$
- 错误。方差是随机变量的固有属性,常数项不会直接累加到方差中,正确形式应为$D(X+C)=D(X)$。
选项C:$D(X-c)=D(X)-c$
- 错误。同理,减去常数项不会改变方差,正确形式应为$D(X-c)=D(X)$,而非减去$c$。
选项D:$D(CX)=CD(X)$
- 错误。根据方差性质,乘以常数$c$时方差应乘以$c^2$,即$D(CX)=C^2D(X)$,而非$CD(X)$。