题目
若(0)=0, lim _(xarrow 0)dfrac (f(2x))(x)=4, 则 '(0)=
若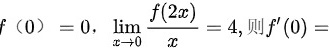
题目解答
答案
解:
∵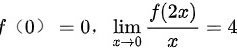
∴对极限变形有:
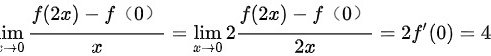
∴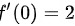
解析
考查要点:本题主要考查导数的定义及其应用,以及极限的变形技巧。
解题核心思路:将已知极限条件与导数的定义式联系起来,通过变量替换或变形,将问题转化为导数的计算。
破题关键点:
- 识别导数的结构:观察到极限形式与导数定义式相似,但变量为$2x$而非$x$,需通过变形统一变量。
- 极限变形:将$\lim_{x \to 0} \frac{f(2x)}{x}$转化为与$f'(0)$相关的表达式,利用$f(0)=0$简化分子。
步骤1:关联导数定义
根据导数定义,$f'(0) = \lim_{h \to 0} \frac{f(h) - f(0)}{h}$。题目中给出$\lim_{x \to 0} \frac{f(2x)}{x} = 4$,且$f(0)=0$,因此分子可改写为$f(2x) - f(0)$。
步骤2:变形极限表达式
将原极限改写为:
$\lim_{x \to 0} \frac{f(2x) - f(0)}{x} = 4.$
将分母$x$拆分为$2x \cdot 2$,即:
$\lim_{x \to 0} \left( \frac{f(2x) - f(0)}{2x} \cdot 2 \right) = 4.$
步骤3:提取导数
注意到$\lim_{x \to 0} \frac{f(2x) - f(0)}{2x} = f'(0)$(因$2x \to 0$),代入得:
$2f'(0) = 4 \quad \Rightarrow \quad f'(0) = 2.$