题目
把长度为a的棒任意折成三段,求它们可以构成一个三角形的概率?
把长度为a的棒任意折成三段,求它们可以构成一个三角形的概率?
题目解答
答案
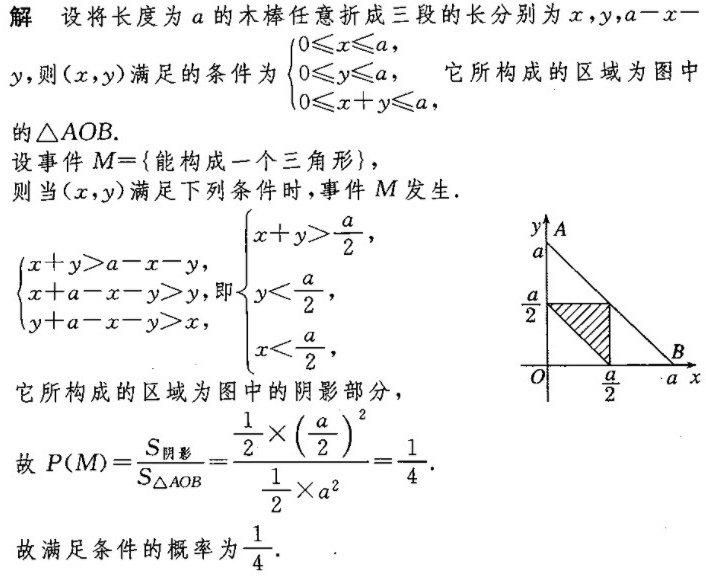
解析
考查要点:本题主要考查几何概率模型的应用,以及三角形构成条件的理解。
解题核心思路:将折断木棒的位置转化为二维平面上的点,利用几何区域面积比计算概率。
破题关键点:
- 三角形构成条件:三段中任意一段必须小于总长度的一半(即$a/2$)。
- 几何模型建立:通过变量$x$和$y$表示两段长度,约束条件转化为区域面积问题。
- 区域面积计算:确定满足条件的区域形状,计算其面积与样本空间面积的比值。
步骤1:建立几何模型
设木棒折成三段的长度分别为$x$、$y$、$a-x-y$,则$x \geq 0$,$y \geq 0$,$x + y \leq a$。所有可能的$(x, y)$构成的区域为直角三角形$D$,顶点在$(0,0)$、$(a,0)$、$(0,a)$,面积为$\frac{a^2}{2}$。
步骤2:确定三角形构成条件
三段能构成三角形需满足:
$\begin{cases}x < \dfrac{a}{2}, \\y < \dfrac{a}{2}, \\a - x - y < \dfrac{a}{2}.\end{cases}$
第三个不等式等价于$x + y > \dfrac{a}{2}$。
步骤3:确定有效区域
满足条件的区域为$D$内同时满足:
- $x < \dfrac{a}{2}$,$y < \dfrac{a}{2}$(形成边长为$\dfrac{a}{2}$的正方形);
- $x + y > \dfrac{a}{2}$(正方形内位于直线$x + y = \dfrac{a}{2}$上方的部分)。
该区域为等腰直角三角形,直角边长为$\dfrac{a}{2}$,面积为$\dfrac{1}{2} \cdot \dfrac{a}{2} \cdot \dfrac{a}{2} = \dfrac{a^2}{8}$。
步骤4:计算概率
概率为有效区域面积与样本空间面积的比值:
$P = \dfrac{\dfrac{a^2}{8}}{\dfrac{a^2}{2}} = \dfrac{1}{4}.$