题目
化简表达式dfrac ({x)^2(y)^2-2xy}(xy)
化简表达式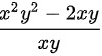
题目解答
答案
根据表达式的值,可知分子和分母均含有x,y因子,因此可以对其分子和分母同时除以xy,化简得到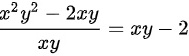 。
。
解析
考查要点:本题主要考查分式的化简,涉及因式分解和约分的基本方法。
解题思路:观察分子和分母的公因式,通过提取公因式或拆分项的方式进行约分,从而简化表达式。
关键点:识别分子中的公因子,或将分子拆分为两个分数相减,再分别约分。
步骤1:分解分子
分子为 $x^2 y^2 - 2xy$,其中每一项均含有公因子 $xy$,因此可以提取公因子:
$x^2 y^2 - 2xy = xy(xy - 2).$
步骤2:约分
将分解后的分子与分母 $xy$ 进行约分:
$\frac{xy(xy - 2)}{xy} = xy - 2 \quad (\text{当 } xy \neq 0 \text{ 时}).$
验证方法(拆分项):
将分子拆分为两个分数相减:
$\frac{x^2 y^2}{xy} - \frac{2xy}{xy} = xy - 2.$