题目
求下列函数的二阶导数:-|||-(12) =ln (x+sqrt (1+{x)^2}).

题目解答
答案
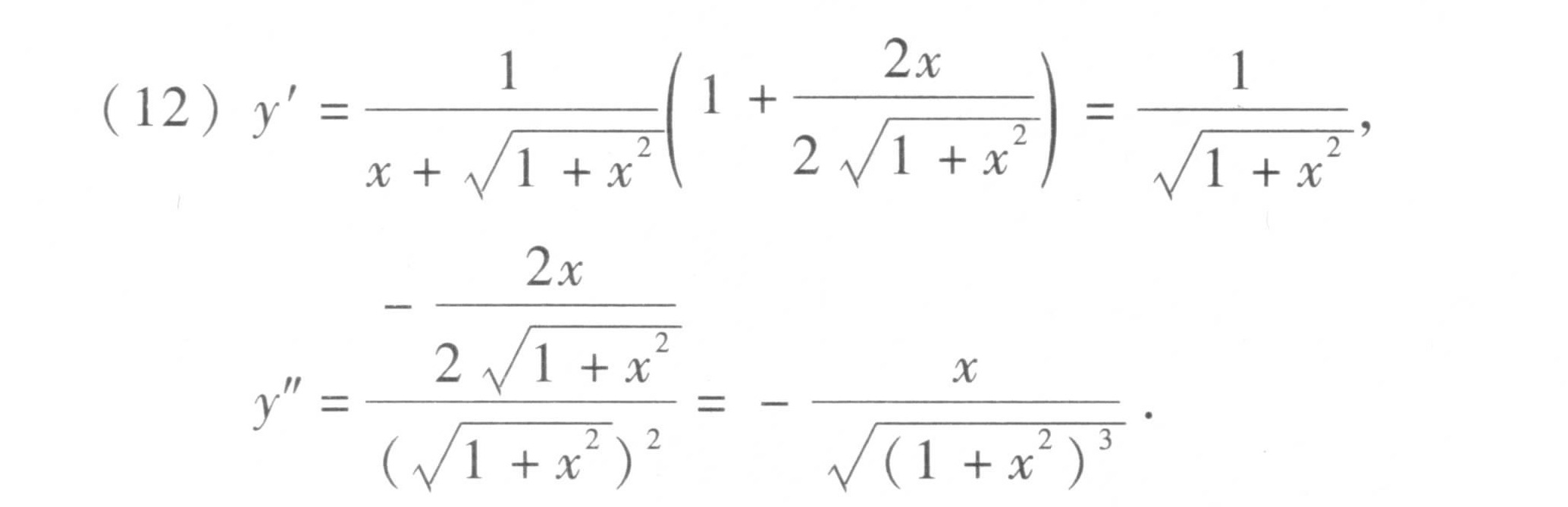
解析
考查要点:本题主要考查复合函数的导数计算,特别是自然对数函数与根式复合后的求导,以及二阶导数的求解方法。
解题核心思路:
- 链式法则:对复合函数逐层求导,注意内外层函数的导数相乘。
- 化简技巧:在一阶导数阶段通过代数变形简化表达式,为后续求二阶导数创造条件。
- 商的导数法则:在求二阶导数时,可能需要处理分式形式的导数。
破题关键点:
- 识别函数结构:外层是自然对数函数,内层是$x + \sqrt{1+x^2}$。
- 化简一阶导数:利用分子分母的对称性,将一阶导数化简为更简洁的形式,避免复杂计算。
第(12)题
求一阶导数$y'$
设$y = \ln(x + \sqrt{1+x^2})$,根据链式法则:
$y' = \frac{1}{x + \sqrt{1+x^2}} \cdot \left(1 + \frac{d}{dx}\sqrt{1+x^2}\right)$
计算$\frac{d}{dx}\sqrt{1+x^2}$:
$\frac{d}{dx}\sqrt{1+x^2} = \frac{1}{2\sqrt{1+x^2}} \cdot 2x = \frac{x}{\sqrt{1+x^2}}$
代入原式:
$y' = \frac{1}{x + \sqrt{1+x^2}} \left(1 + \frac{x}{\sqrt{1+x^2}}\right)$
化简表达式:
分子通分:
$1 + \frac{x}{\sqrt{1+x^2}} = \frac{\sqrt{1+x^2} + x}{\sqrt{1+x^2}}$
分母为$x + \sqrt{1+x^2}$,与分子约分:
$y' = \frac{\sqrt{1+x^2} + x}{\sqrt{1+x^2} \cdot (x + \sqrt{1+x^2})} = \frac{1}{\sqrt{1+x^2}}$
求二阶导数$y''$
对$y' = (1+x^2)^{-1/2}$应用链式法则:
$y'' = -\frac{1}{2}(1+x^2)^{-3/2} \cdot 2x = -\frac{x}{(1+x^2)^{3/2}}$