题目
包含零向量的向量组是线性相关的()A.正确B.错误
包含零向量的向量组是线性相关的()
A.正确
B.错误
题目解答
答案
若一个向量组包含零向量
则此零向量可由任意向量线性组合进行表示
而线性相关的定义即为向量组中存在向量可由其他向量表示,则向量组线性相关
∴包含零向量的向量组是线性相关的
即命题正确
即本题答案为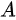
解析
考查要点:本题主要考查向量组线性相关的定义及其与零向量的关系。
解题核心思路:
根据线性相关的定义,若向量组中存在至少一个向量可以被其他向量线性表示,则该向量组线性相关。关键点在于零向量的特殊性:零向量本身可以由其他向量(包括自身)的线性组合表示,且这种表示不需要其他向量的存在。因此,只要向量组包含零向量,即可直接判定其线性相关。
破题关键:
- 零向量的性质:零向量可以表示为任意系数组合(如全零系数加自身系数为1)的结果。
- 线性相关定义的直接应用:零向量的存在使得存在非全零系数的线性组合等于零向量。
题目分析:
若向量组中包含零向量,则该零向量可以被其他向量(包括自身)线性组合表示。例如,设向量组为 $\{\mathbf{v}_1, \mathbf{v}_2, \dots, \mathbf{v}_n, \mathbf{0}\}$,则存在系数 $k_1=0, k_2=0, \dots, k_n=0, k_{n+1}=1$,使得:
$k_1\mathbf{v}_1 + k_2\mathbf{v}_2 + \dots + k_n\mathbf{v}_n + k_{n+1}\mathbf{0} = \mathbf{0}$
此时系数不全为零($k_{n+1}=1$),满足线性相关的定义。因此命题正确。