题目
设f(x)对任意实数x,y,有f(x+y)=f(x)+f(y),且f(x)在x=0连续,证明:f(x)在R上连续.
设f(x)对任意实数x,y,有f(x+y)=f(x)+f(y),且f(x)在x=0连续,证明:f(x)在R上连续.
题目解答
答案
证明:由于f(x)在x=0连续,因此 ,又因为f(x+y)=f(x)+f(y),在R上任取一点
,又因为f(x+y)=f(x)+f(y),在R上任取一点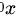 ,则
,则
 ,所以f(x)在
,所以f(x)在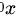 处连续,所以f(x)在R上连续.
处连续,所以f(x)在R上连续.
解析
考查要点:本题主要考查加性函数(Cauchy函数)的连续性性质,以及如何利用已知的局部连续性推导全局连续性。
解题核心思路:
- 利用加性函数的性质:由$f(x+y)=f(x)+f(y)$可推出$f(0)=0$,并进一步得到$f$的线性结构(在连续条件下)。
- 局部连续性推广到全局:已知$f$在$x=0$处连续,通过变量替换和极限运算,证明$f$在任意点$x_0$处连续。
破题关键点:
- 关键结论:加性函数若在某一点连续,则在全体实数上连续。
- 关键方法:通过变量替换$h = x - x_0$,将任意点$x_0$的连续性问题转化为$x=0$处的连续性问题。
步骤1:确定$f(0)$的值
由$f(x+y)=f(x)+f(y)$,令$x=y=0$,得:
$f(0+0)=f(0)+f(0) \implies f(0)=2f(0) \implies f(0)=0.$
步骤2:利用$x=0$处的连续性
已知$f$在$x=0$处连续,故:
$\lim_{x \to 0} f(x) = f(0) = 0.$
步骤3:证明任意点$x_0$处的连续性
任取$x_0 \in \mathbb{R}$,考虑$x \to x_0$时的极限。令$x = x_0 + h$,当$h \to 0$时,$x \to x_0$。根据加性函数性质:
$f(x) = f(x_0 + h) = f(x_0) + f(h).$
当$h \to 0$时,$f(h) \to f(0) = 0$(由步骤2),因此:
$\lim_{h \to 0} f(x_0 + h) = f(x_0) + 0 = f(x_0).$
这表明$f$在$x_0$处连续。
结论:$f(x)$在$\mathbb{R}$上连续。