题目
已知非齐次线性方程组 Ax= β有解,则下列结论中错误的是() A 增广矩阵Ax= β 的列向量组线性相关 B 齐次线方组Ax= β必有非零解 C 增广矩阵 Ax= β的秩等于系数矩阵A的秩D Ax= β可由Ax= β的列向量组线性表示
已知非齐次线性方程组 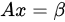 有解,则下列结论中错误的是()
有解,则下列结论中错误的是()
A 增广矩阵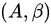 的列向量组线性相关
的列向量组线性相关
B 齐次线方组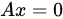 必有非零解
必有非零解
C 增广矩阵 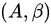 的秩等于系数矩阵A的秩
的秩等于系数矩阵A的秩
D 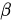 可由
可由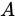 的列向量组线性表示
的列向量组线性表示
题目解答
答案
A项,若非齐次线性方程组 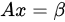 有解,则增广矩阵
有解,则增广矩阵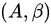 的列向量组线性相关 ,故A项正确;
的列向量组线性相关 ,故A项正确;
B项,若非齐次线性方程组 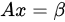 有解,则
有解,则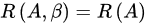 ,但不一定齐次线方组
,但不一定齐次线方组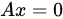 非零解 ,故B项错误;
非零解 ,故B项错误;
C项,若非齐次线性方程组 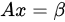 有解,则增广矩阵
有解,则增广矩阵 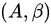 的秩等于系数矩阵A的秩,故C项正确;
的秩等于系数矩阵A的秩,故C项正确;
D项,若非齐次线性方程组 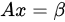 有解,则
有解,则 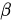 可由
可由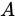 的列向量组线性表示,故D项正确;
的列向量组线性表示,故D项正确;
因此,答案为B。
解析
考查要点:本题主要考查非齐次线性方程组解的判定定理及其相关性质,涉及增广矩阵秩的关系、列向量组的线性相关性、齐次方程组解的结构等核心概念。
解题思路:
- 明确非齐次方程组有解的充要条件:增广矩阵的秩等于系数矩阵的秩,即$R(A,β)=R(A)$。
- 分析各选项与条件的关系:
- 选项A:增广矩阵列向量组线性相关,由方程组有解可直接推出。
- 选项B:齐次方程组必有非零解,需结合系数矩阵秩与未知数个数的关系,但题目未提供足够信息。
- 选项C:秩相等是已知条件的直接结论。
- 选项D:方程组有解的本质即β可由A的列向量线性表示。
- 关键矛盾点:选项B的成立需要额外条件($R(A) < n$),而题目未明确该条件,因此可能错误。
选项分析
选项A
非齐次方程组有解时,增广矩阵$(A,β)$的秩等于$A$的秩,说明β可由$A$的列向量线性表示。因此,增广矩阵的列向量组(比$A$多一列β)必然线性相关。选项A正确。
选项B
齐次方程组$Ax=0$有非零解的充要条件是$R(A) < n$($n$为未知数个数)。但题目仅给出非齐次方程组有解(即$R(A,β)=R(A)$),未说明$R(A)$是否小于$n$。例如,若$A$为满秩矩阵(如$R(A)=n$),则齐次方程组仅有零解。选项B不一定成立,故错误。
选项C
非齐次方程组有解的充要条件即为$R(A,β)=R(A)$,这是题目已知条件的直接结论。选项C正确。
选项D
非齐次方程组有解的本质含义是β可由$A$的列向量线性表示,这是方程组有解的定义。选项D正确。