2.计算下列极限:-|||-(1) lim _(xarrow 0)((1-x))^dfrac (1{x)} :-|||-(3) lim _(xarrow infty )((dfrac {1+x)(x))}^2x =-|||-(2) lim _(xarrow 0)((1+2x))^dfrac (1{x)} :-|||-(4) lim _(xarrow infty )((1-dfrac {1)(x))}^kx (k为正整数).
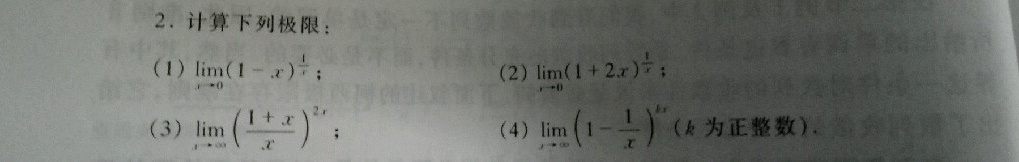
题目解答
答案
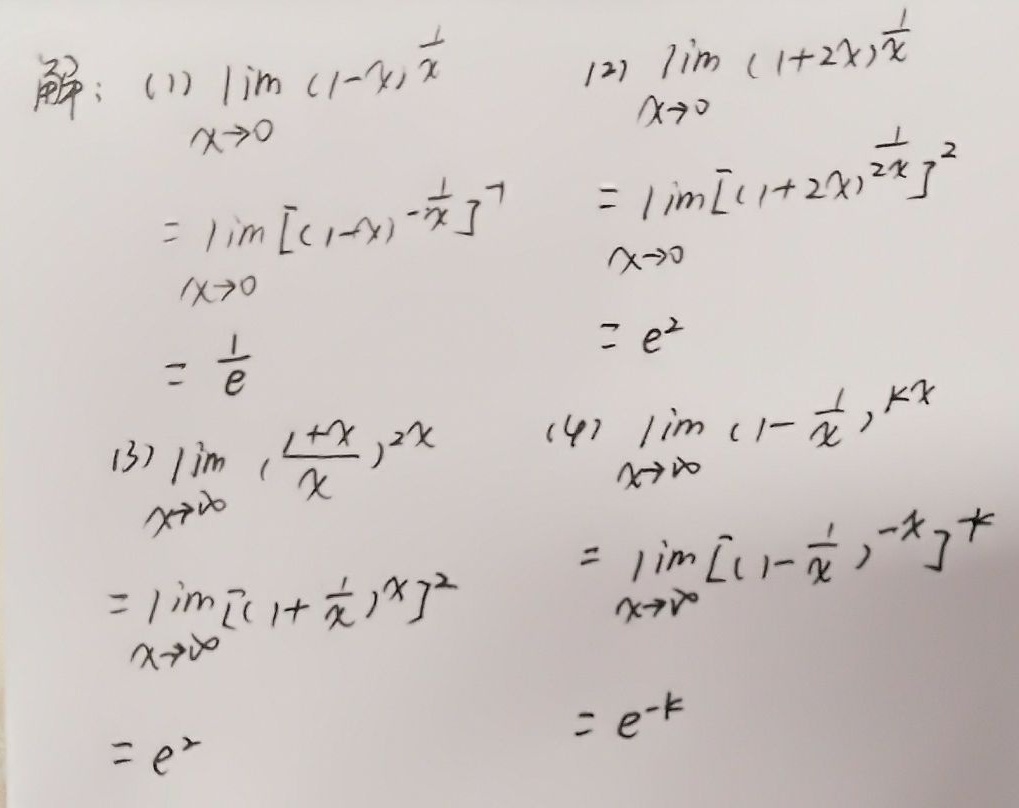
解析
本题考查重要极限公式的应用,特别是自然对数的底数$e$的表达式。解题核心思路是将题目中的表达式转化为标准形式$\lim_{x \to 0} (1 + ax)^{\frac{1}{x}} = e^a$或$\lim_{x \to \infty} \left(1 + \frac{b}{x}\right)^x = e^b$,通过调整指数和底数的对应关系求解。
第(1)题
转化为标准形式
原式$\lim_{x \to 0} (1 - x)^{\frac{1}{x}}$可视为$\lim_{x \to 0} \left(1 + (-x)\right)^{\frac{1}{x}}$,对应$a = -1$。
应用重要极限
根据公式$\lim_{x \to 0} (1 + ax)^{\frac{1}{x}} = e^a$,直接得结果为$e^{-1}$。
第(2)题
转化为标准形式
原式$\lim_{x \to 0} (1 + 2x)^{\frac{1}{x}}$对应$a = 2$。
应用重要极限
根据公式得结果为$e^{2}$。
第(3)题
化简表达式
原式$\lim_{x \to \infty} \left(\frac{1 + x}{x}\right)^{2x} = \lim_{x \to \infty} \left(1 + \frac{1}{x}\right)^{2x}$。
应用重要极限
根据$\lim_{x \to \infty} \left(1 + \frac{1}{x}\right)^x = e$,得$\left[\lim_{x \to \infty} \left(1 + \frac{1}{x}\right)^x\right]^2 = e^2$。
第(4)题
转化为标准形式
原式$\lim_{x \to \infty} \left(1 - \frac{1}{x}\right)^{kx} = \left[\lim_{x \to \infty} \left(1 - \frac{1}{x}\right)^x\right]^k$。
应用重要极限
根据$\lim_{x \to \infty} \left(1 - \frac{1}{x}\right)^x = e^{-1}$,得$\left(e^{-1}\right)^k = e^{-k}$。