题目
求极限lim _(xarrow 0)dfrac ({e)^(x^2)-(e)^2-2cos x}({x)^4}
求极限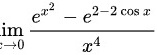
题目解答
答案
答案: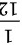
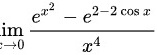
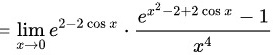
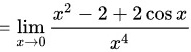
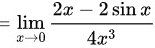
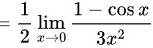
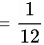
解析
步骤 1:应用洛必达法则
首先,观察到当$x\rightarrow 0$时,分子和分母都趋向于0,因此可以应用洛必达法则。洛必达法则用于求解形如$\frac{0}{0}$或$\frac{\infty}{\infty}$的极限问题,通过求导数来简化极限的计算。
步骤 2:对分子和分母求导
对分子${e}^{{x}^{2}}-{e}^{2-2\cos x}$和分母${x}^{4}$分别求导,得到新的极限形式。
步骤 3:简化极限表达式
通过求导简化后的极限表达式,继续应用洛必达法则,直到可以求出极限值。
步骤 4:计算最终极限值
通过多次应用洛必达法则,最终求出极限值。
首先,观察到当$x\rightarrow 0$时,分子和分母都趋向于0,因此可以应用洛必达法则。洛必达法则用于求解形如$\frac{0}{0}$或$\frac{\infty}{\infty}$的极限问题,通过求导数来简化极限的计算。
步骤 2:对分子和分母求导
对分子${e}^{{x}^{2}}-{e}^{2-2\cos x}$和分母${x}^{4}$分别求导,得到新的极限形式。
步骤 3:简化极限表达式
通过求导简化后的极限表达式,继续应用洛必达法则,直到可以求出极限值。
步骤 4:计算最终极限值
通过多次应用洛必达法则,最终求出极限值。