有一大批产品,其验收方案如下,先作第一次检验:从中任取10件,经检验无次品时接受这批产品,次品数大于2时拒收;否则作第二次检验,其做法是从中再任取5件,仅当5件中无次品时接受这批产品.若产品的次品率为10%,求(1) 这批产品经第一次检验就能接受的概率.(2)需作第二次检验的概率.(3)这批产品按第二次检验的标准被接受的概率.(4) 这批产品在第一次检验未能作决定且第二次检验时被通过的概率.(5)这批产品被接受的概率.
有一大批产品,其验收方案如下,先作第一次检验:从中任取10件,经检验无次品时接受这批产品,次品数大于2时拒收;否则作第二次检验,其做法是从中再任取5件,仅当5件中无次品时接受这批产品.若产品的次品率为10%,求
(1) 这批产品经第一次检验就能接受的概率.
(2)需作第二次检验的概率.
(3)这批产品按第二次检验的标准被接受的概率.
(4) 这批产品在第一次检验未能作决定且第二次检验时被通过的概率.
(5)这批产品被接受的概率.
题目解答
答案
解:若以 X表示所抽得的 10件产品中所含的次品数,则X~B(10,0.1);又若以Y表示第二次抽检中出现的次品数,则Y~B(5,0.1).
(1)按题意所求概率为
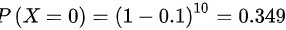
(2) 需作第二次检验的概率为
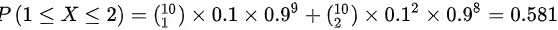
(3)按第二次检验标准接受这批产品的概率为
P{Y = 0} = 0.9⁵ = 0.590
(4)所求概率为
P{(1≤X≤2)∩(Y=0)}.
因为X,Y的取值被认为是放回抽样的结果,即都是独立试验的结果,因此,事件{1≤X≤2}与{Y=0}是相互独立的,从而
P{(1≤X≤2)∩(Y=0)}=P{1≤X≤2}P{Y=0}=0.581×0.590 = 0.343
(5)这批产品被接受的概率为
P{(X=0)∪[(1≤X≤2)∩(Y=0)]}=P{X=0}+P{(1≤X≤2)∩(Y=0)}
=0.349+0.343=0.692
解析
考查要点:本题主要考查二项分布的概率计算以及事件独立性的应用,涉及多个阶段的条件概率分析。
解题核心思路:
- 明确各阶段检验规则,确定对应概率事件;
- 识别随机变量分布:第一次检验次品数$X \sim B(10,0.1)$,第二次检验次品数$Y \sim B(5,0.1)$;
- 区分独立事件与互斥事件,合理拆分复合事件的概率计算。
破题关键点:
- 第(1)题:直接计算$X=0$的概率;
- 第(2)题:计算$X=1$或$X=2$的概率之和;
- 第(3)题:计算$Y=0$的概率;
- 第(4)题:利用独立性,将$1 \leq X \leq 2$与$Y=0$的概率相乘;
- 第(5)题:合并互斥事件(第一次直接接受或两次检验后接受)的概率。
第(1)题
目标:第一次检验无次品的概率。
步骤:
- 确定事件:$X=0$(10件中无次品);
- 二项分布公式:
$P(X=0) = \binom{10}{0} \cdot (0.1)^0 \cdot (0.9)^{10} = 0.9^{10} \approx 0.349.$
第(2)题
目标:需第二次检验的概率(即$1 \leq X \leq 2$)。
步骤:
- 拆分事件:$X=1$和$X=2$;
- 分别计算概率:
- $P(X=1) = \binom{10}{1} \cdot (0.1)^1 \cdot (0.9)^9 \approx 0.387$;
- $P(X=2) = \binom{10}{2} \cdot (0.1)^2 \cdot (0.9)^8 \approx 0.194$;
- 求和:
$P(1 \leq X \leq 2) = 0.387 + 0.194 = 0.581.$
第(3)题
目标:第二次检验无次品的概率。
步骤:
- 确定事件:$Y=0$(5件中无次品);
- 二项分布公式:
$P(Y=0) = 0.9^5 \approx 0.590.$
第(4)题
目标:第一次未决且第二次通过的概率。
步骤:
- 独立性判断:两次检验相互独立;
- 联合概率公式:
$P(1 \leq X \leq 2 \text{ 且 } Y=0) = P(1 \leq X \leq 2) \cdot P(Y=0) = 0.581 \cdot 0.590 \approx 0.343.$
第(5)题
目标:总接受概率。
步骤:
- 拆分路径:
- 直接接受($X=0$);
- 两次检验后接受($1 \leq X \leq 2$且$Y=0$);
- 互斥事件求和:
$P(\text{接受}) = P(X=0) + P(1 \leq X \leq 2 \text{ 且 } Y=0) = 0.349 + 0.343 = 0.692.$