题目
一袋中装有5只球，编号为1,2,3,4,5.在袋中同时取3只，以X表示取出的3只球中的最大号码，求随机变量X的分布律。
一袋中装有5只球，编号为1,2,3,4,5.在袋中同时取3只，以X表示取出的3只球中的最大号码，求随机变量X的分布律。
题目解答
答案
由题意知，随机变量X的取值为3,4,5.
当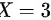
时，即取出的三只球最大号码为3，另外两个球一定是1,2。所以，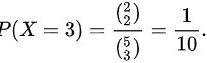
当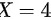
时，即取出的三只球最大号码为3，另外两个球在1,2,3中取得。所以，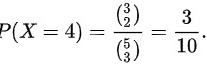
当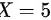
时，即取出的三只球最大号码为3，另外两个球在1,2,3，4中取得。所以，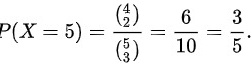
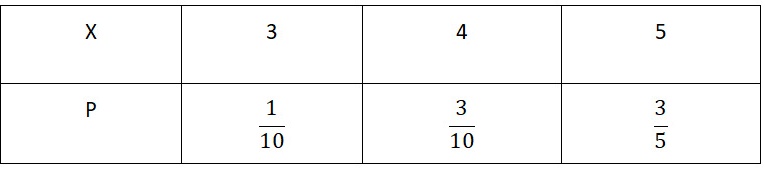
因此，随机变量X的分布律如下，
解析
步骤 1：确定随机变量X的取值范围
随机变量X表示取出的3只球中的最大号码，因此X的取值范围为3,4,5。
步骤 2：计算P(X=3)
当X=3时，即取出的三只球最大号码为3，另外两个球一定是1,2。所以，$P(X=3)=\dfrac {(\dfrac {2}{2})}{(\dfrac {5}{3})}=\dfrac {1}{10}$
步骤 3：计算P(X=4)
当X=4时，即取出的三只球最大号码为4，另外两个球在1,2,3中取得。所以，$P(X=4)=\dfrac {(\dfrac {3}{2})}{(\dfrac {5}{3})}=\dfrac {3}{10}$
步骤 4：计算P(X=5)
当X=5时，即取出的三只球最大号码为5，另外两个球在1,2,3，4中取得。所以，$P(X=5)=\dfrac {(\dfrac {4}{2})}{(\dfrac {5}{3})}=\dfrac {6}{10}=\dfrac {3}{5}$
随机变量X表示取出的3只球中的最大号码，因此X的取值范围为3,4,5。
步骤 2：计算P(X=3)
当X=3时，即取出的三只球最大号码为3，另外两个球一定是1,2。所以，$P(X=3)=\dfrac {(\dfrac {2}{2})}{(\dfrac {5}{3})}=\dfrac {1}{10}$
步骤 3：计算P(X=4)
当X=4时，即取出的三只球最大号码为4，另外两个球在1,2,3中取得。所以，$P(X=4)=\dfrac {(\dfrac {3}{2})}{(\dfrac {5}{3})}=\dfrac {3}{10}$
步骤 4：计算P(X=5)
当X=5时，即取出的三只球最大号码为5，另外两个球在1,2,3，4中取得。所以，$P(X=5)=\dfrac {(\dfrac {4}{2})}{(\dfrac {5}{3})}=\dfrac {6}{10}=\dfrac {3}{5}$