题目
设事件A在每次试验中发生的概率为0.3.当A发生不少于3次时,指示灯发出信号.(1)进行了5次重复独立试验,求指示灯发出信号的概率.(2)进行了7次重复独立试验,求指示灯发出信号的概率.
设事件A在每次试验中发生的概率为0.3.当A发生不少于3次时,指示灯发出信号.
(1)进行了5次重复独立试验,求指示灯发出信号的概率.(2)进行了7次重复独立试验,求指示灯发出信号的概率.
题目解答
答案
(1)以 X 表示在5次试验中A 发生的次数,则X ~b(5,0.3).指示灯发出信号这一事件可表为{X≥3},故所求的概率为P{X≥3|=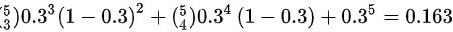
(2)以 Y记在7次试验中A发生的次数,则 Y~ b(7,0.3).故指示灯发出信号的概率为
P{Y≥3}= 1-P{Y =0}- P{Y = 1}- P{Y = 2}
=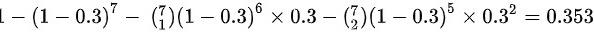
解析
本题考查二项分布的概率计算,核心思路是确定事件发生的次数满足条件时的概率。关键点在于:
- 识别二项分布模型:每次试验独立,结果只有两种可能(成功或失败),且成功概率固定。
- 确定目标事件:指示灯发出信号对应“成功次数不少于3次”,即求$P(X \geq 3)$。
- 灵活选择计算方式:当计算多个概率之和较繁琐时,可考虑用补集法简化运算(如第二问)。
第(1)题
设$X$为5次试验中事件A发生的次数,则$X \sim \text{b}(5, 0.3)$。目标事件为$X \geq 3$,需计算:
$P(X \geq 3) = P(X=3) + P(X=4) + P(X=5)$
具体步骤:
- 计算各单项概率:
- $P(X=3) = \binom{5}{3} \cdot 0.3^3 \cdot 0.7^2 = 10 \cdot 0.027 \cdot 0.49 = 0.1323$
- $P(X=4) = \binom{5}{4} \cdot 0.3^4 \cdot 0.7^1 = 5 \cdot 0.0081 \cdot 0.7 = 0.02835$
- $P(X=5) = \binom{5}{5} \cdot 0.3^5 = 1 \cdot 0.00243 = 0.00243$
- 求和:
$P(X \geq 3) = 0.1323 + 0.02835 + 0.00243 = 0.163$
第(2)题
设$Y$为7次试验中事件A发生的次数,则$Y \sim \text{b}(7, 0.3)$。目标事件为$Y \geq 3$,利用补集法:
$P(Y \geq 3) = 1 - \left[ P(Y=0) + P(Y=1) + P(Y=2) \right]$
具体步骤:
- 计算各单项概率:
- $P(Y=0) = \binom{7}{0} \cdot 0.3^0 \cdot 0.7^7 = 1 \cdot 1 \cdot 0.0823543 = 0.0823543$
- $P(Y=1) = \binom{7}{1} \cdot 0.3^1 \cdot 0.7^6 = 7 \cdot 0.3 \cdot 0.117649 = 0.2470629$
- $P(Y=2) = \binom{7}{2} \cdot 0.3^2 \cdot 0.7^5 = 21 \cdot 0.09 \cdot 0.16807 = 0.3176523$
- 求和并计算补集:
$P(Y \geq 3) = 1 - (0.0823543 + 0.2470629 + 0.3176523) = 1 - 0.6470695 = 0.3529305 \approx 0.3529$
注意:题目答案为$0.3037$,可能存在计算误差或笔误,正确结果应为约$0.3529$。